Lunar Eclipse Statistics
Fred Espenak
This page is based on information published in the Five Millennium Canon of Lunar Eclipses: -1999 to +3000 and the Five Millennium Catalog of Lunar Eclipses: -1999 to +3000.
1.1 Statistical Distribution of Lunar Eclipse Types
Eclipses of the Moon can only occur during the Full Moon phase. It is then possible for the Moon to pass through Earth’s penumbral and umbral shadows thereby producing an eclipse. There are three types of lunar eclipses:
- Penumbral – Moon passes partially or completely into Earth’s penumbral shadow.
- Partial – Moon passes partially into Earth’s umbral shadow.
- Total – Moon passes completely into Earth’s umbral shadow.
During the 5,000-year period from –1999 to +3000 (2000 BCE to 3000 CE [1]), Earth will experience 12,064 eclipses of the Moon. The statistical distribution of the three eclipse types over this interval is shown in Table 1.
| Table 1: Distribution of Three Lunar Eclipse Types from –1999 to +3000 (2000 BCE to 3000 CE) |
|||
| Eclipse Type | Abbreviation | Number of Eclipses |
Percent |
| All Eclipses | – | 12064 | 100.0% |
| Penumbral | N | 4378 | 36.3% |
| Partial | P | 4207 | 34.9% |
| Total | T | 3479 | 28.8% |
During most penumbral eclipses, only part of the Moon passes through Earth’s penumbral shadow. Examples of such partial penumbral eclipses include: 2009 Feb 09, 2009 Jul 07, 2009 Aug 06, and 2012 Nov 28. However, it is also possible to have a penumbral eclipse in which the Moon passes completely within Earth’s penumbral shadow without entering the inner umbral shadow. Such total penumbral eclipses are quite rare compared to normal (or partial) penumbral eclipses. During the 21st century, there are 87 partial penumbral eclipses, but only 5 total penumbral eclipses: 2006 Mar 14, 2053 Aug 29, 2070 Apr 25, 2082 Aug 08, and 2099 Sep 29. Table 2 shows the distribution of the two penumbral eclipse types during the period covered by the Canon of Lunar Eclipses. For more on total penumbral eclipses, see Section 1.11.
| Table 2: Statistics of Penumbral Lunar Eclipses from –1999 to +3000 (2000 BCE to 3000 CE) |
||
| Eclipse Type | Number of Eclipses |
Percent |
| All Penumbral Eclipses | 4378 | 100.0% |
| Partial Penumbral | 4237 | 96.8% |
| Total Penumbral | 141 | 3.2% |
Total lunar eclipses through Earth’s umbral shadow can be categorized as:
- Central – The Moon passes through the central axis of Earth’s umbral shadow.
- Non-Central – The Moon misses the central axis of Earth’s umbral shadow.
Using the above categories, the distribution of the 3,479 total eclipses is shown in Table 3.
| Table 3: Statistics of Total Lunar Eclipses from –1999 to +3000 (2000 BCE to 3000 CE) |
||
| Eclipse Type | Number of Eclipses |
Percent |
| All Total Eclipses | 3479 | 100.0% |
| Central Total | 2074 | 59.6% |
| Non-Central Total | 1405 | 40.4% |
Examples of central total eclipses include: 2000 Jul 16, 2011 Jun 15, 2018 Jul 27, and 2022 May 16. Several examples of non-central total eclipses are: 2010 Dec 21, 2011 Dec 10, 2014 Apr 15, and 2014 Oct 08.
Footnotes
[1] The terms BCE and CE are abbreviations for "Before Common Era" and "Common Era," respectively. They are the secular equivalents to the BC and AD dating conventions. (See: Year Dating Conventions)
1.2 Distribution of Lunar Eclipse Types by Century
Table 4 summarizes 5,000 years of eclipses by eclipse type over 100-year intervals. The average century contains 241 lunar eclipses of which 88 are penumbral, 84 are partial and 70 are total. Individual centuries deviate from these mean values in interesting ways. For instance, the total number of eclipses in a century varies from a minimum of 225 (century beginning –0899) to a maximum of 259 (centuries beginning 1101 and 2801). The number of penumbral eclipses varies from 76 (century 0301) to 100 (century 2801), while the number of partial eclipses ranges from 54 (century –1599) to 102 (centuries –0699, 1101, and 2801). Finally, the number of total lunar eclipses per century varies from 57 (centuries 0001 and 2801) to 89 (century 0801). Note that century 2801 not only has the most number of eclipses (259), it also has the maximum number of penumbral (100) and partial (102) eclipses, but the minimum number of total eclipses (57).
The last column of Table 4 lists the number of total lunar eclipse tetrads per century. A tetrad is a grouping of four consecutive total lunar eclipses each separated by six lunations. Their frequency is quite variable with some centuries having 0 tetrads, while others may have as many as 8. For more on tetrads, see Section 1.16.
When the data in Table 4 is displayed graphically in Figure 1, other important relationships are revealed. The most apparent feature is a periodic oscillation in the number of all lunar eclipses (Figure 1a), as well as in the individual types. By inspection, the period is about 600 years. Using tables from von Oppolzer's Canon der Finsternisse (1887) the Dutch astronomer G. van den Bergh (1954) calculated a period of 586 years. By studying the distributions of tetrad eclipse groups (Section 1.16), Meeus derived an empirical expression showing that this period is slowly decreasing (Meeus 2004b). While its current value is actually 565 years, the period was 618 years in –1999 and it will decrease to 552 years by +3000. A theoretical study by T. Hughes (Hughes 2004) demonstrates that the period is caused by the eccentricity of Earth’s orbit, which is gradually decreasing.
There are other interesting features in Figure 1. For instance, the number of total lunar eclipses as well as deep central total eclipses is highest when the number of all lunar eclipses is at a minimum. In contrast, numbers of penumbral eclipses, partial eclipses and non-central total eclipses all appear to be synchronized with the overall number of lunar eclipses. Finally, the number of total penumbral eclipses, and total lunar eclipse tetrads are most frequent during epochs when the overall number of lunar eclipses is at a minimum.
| Table 4: Lunar Eclipse Types by Century: –1999 to +3000 (2000 BCE to 3000 CE) |
|||||||||
| Century Interval | All Lunar Eclipses |
All Penum. Eclipses |
Partial Penum. Eclipses |
Total Penum. Eclipses |
All Partial Eclipses* |
All Total Eclipses |
Central Total Eclipses |
Non- Central Total Eclipses |
Total Eclipse Tetrads |
| -1999 to -1900 | 242 | 88 | 84 | 4 | 92 | 62 | 13 | 49 | 1 |
| -1899 to -1800 | 255 | 98 | 97 | 1 | 97 | 60 | 11 | 49 | 0 |
| -1799 to -1700 | 254 | 94 | 94 | 0 | 99 | 61 | 12 | 49 | 0 |
| -1699 to -1600 | 244 | 90 | 87 | 3 | 87 | 67 | 21 | 46 | 3 |
| -1599 to -1500 | 226 | 85 | 81 | 4 | 54 | 87 | 62 | 25 | 8 |
| -1499 to -1400 | 228 | 86 | 78 | 8 | 60 | 82 | 55 | 27 | 6 |
| -1399 to -1300 | 239 | 83 | 80 | 3 | 90 | 66 | 23 | 43 | 2 |
| -1299 to -1200 | 251 | 92 | 91 | 1 | 99 | 60 | 9 | 51 | 0 |
| -1199 to -1100 | 252 | 96 | 95 | 1 | 95 | 61 | 13 | 48 | 0 |
| -1099 to -1000 | 240 | 88 | 81 | 7 | 86 | 66 | 18 | 48 | 4 |
| -0999 to -0900 | 228 | 80 | 72 | 8 | 61 | 87 | 59 | 28 | 7 |
| -0899 to -0800 | 225 | 79 | 76 | 3 | 62 | 84 | 57 | 27 | 7 |
| -0799 to -0700 | 239 | 87 | 85 | 2 | 88 | 64 | 21 | 43 | 1 |
| -0699 to -0600 | 253 | 91 | 91 | 0 | 102 | 60 | 10 | 50 | 0 |
| -0599 to -0500 | 255 | 95 | 95 | 0 | 100 | 60 | 11 | 49 | 0 |
| -0499 to -0400 | 242 | 88 | 86 | 2 | 90 | 64 | 19 | 45 | 1 |
| -0399 to -0300 | 229 | 80 | 79 | 1 | 61 | 88 | 54 | 34 | 7 |
| -0299 to -0200 | 228 | 79 | 76 | 3 | 64 | 85 | 55 | 30 | 6 |
| -0199 to -0100 | 240 | 85 | 84 | 1 | 86 | 69 | 21 | 48 | 3 |
| -0099 to 0000 | 253 | 94 | 93 | 1 | 98 | 61 | 11 | 50 | 0 |
| 0001 to 0100 | 251 | 93 | 92 | 1 | 101 | 57 | 7 | 50 | 0 |
| 0101 to 0200 | 239 | 84 | 82 | 2 | 88 | 67 | 23 | 44 | 3 |
| 0201 to 0300 | 228 | 83 | 75 | 8 | 63 | 82 | 53 | 29 | 6 |
| 0301 to 0400 | 227 | 76 | 72 | 4 | 69 | 82 | 58 | 24 | 4 |
| 0401 to 0500 | 244 | 83 | 82 | 1 | 95 | 66 | 18 | 48 | 3 |
| 0501 to 0600 | 254 | 97 | 96 | 1 | 95 | 62 | 12 | 50 | 0 |
| 0601 to 0700 | 255 | 97 | 94 | 3 | 100 | 58 | 10 | 48 | 0 |
| 0701 to 0800 | 240 | 84 | 82 | 2 | 88 | 68 | 23 | 45 | 3 |
| 0801 to 0900 | 228 | 79 | 74 | 5 | 60 | 89 | 65 | 24 | 8 |
| 0901 to 1000 | 230 | 82 | 79 | 3 | 70 | 78 | 45 | 33 | 6 |
| 1001 to 1100 | 246 | 87 | 84 | 3 | 97 | 62 | 14 | 48 | 0 |
| 1101 to 1200 | 259 | 98 | 98 | 0 | 102 | 59 | 10 | 49 | 0 |
| 1201 to 1300 | 251 | 95 | 94 | 1 | 96 | 60 | 12 | 48 | 0 |
| 1301 to 1400 | 231 | 81 | 73 | 8 | 73 | 77 | 41 | 36 | 6 |
| 1401 to 1500 | 228 | 80 | 77 | 3 | 65 | 83 | 60 | 23 | 4 |
| 1501 to 1600 | 233 | 82 | 79 | 3 | 74 | 77 | 39 | 38 | 6 |
| 1601 to 1700 | 249 | 91 | 88 | 3 | 97 | 61 | 11 | 50 | 0 |
| 1701 to 1800 | 256 | 98 | 98 | 0 | 98 | 60 | 13 | 47 | 0 |
| 1801 to 1900 | 249 | 90 | 88 | 2 | 97 | 62 | 11 | 51 | 0 |
| 1901 to 2000 | 229 | 83 | 74 | 9 | 65 | 81 | 48 | 33 | 5 |
| 2001 to 2100 | 228 | 86 | 81 | 5 | 57 | 85 | 61 | 24 | 8 |
| 2101 to 2200 | 238 | 81 | 77 | 4 | 88 | 69 | 24 | 45 | 4 |
| 2201 to 2300 | 252 | 94 | 93 | 1 | 97 | 61 | 11 | 50 | 0 |
| 2301 to 2400 | 253 | 95 | 95 | 0 | 98 | 60 | 12 | 48 | 0 |
| 2401 to 2500 | 237 | 83 | 77 | 6 | 85 | 69 | 23 | 46 | 4 |
| 2501 to 2600 | 227 | 82 | 77 | 5 | 58 | 87 | 64 | 23 | 8 |
| 2601 to 2700 | 230 | 81 | 80 | 1 | 70 | 79 | 44 | 35 | 7 |
| 2701 to 2800 | 241 | 86 | 83 | 3 | 91 | 64 | 16 | 48 | 0 |
| 2801 to 2900 | 259 | 100 | 99 | 1 | 102 | 57 | 9 | 48 | 0 |
| 2901 to 3000 | 249 | 89 | 89 | 0 | 97 | 63 | 13 | 50 | 1 |
![]()
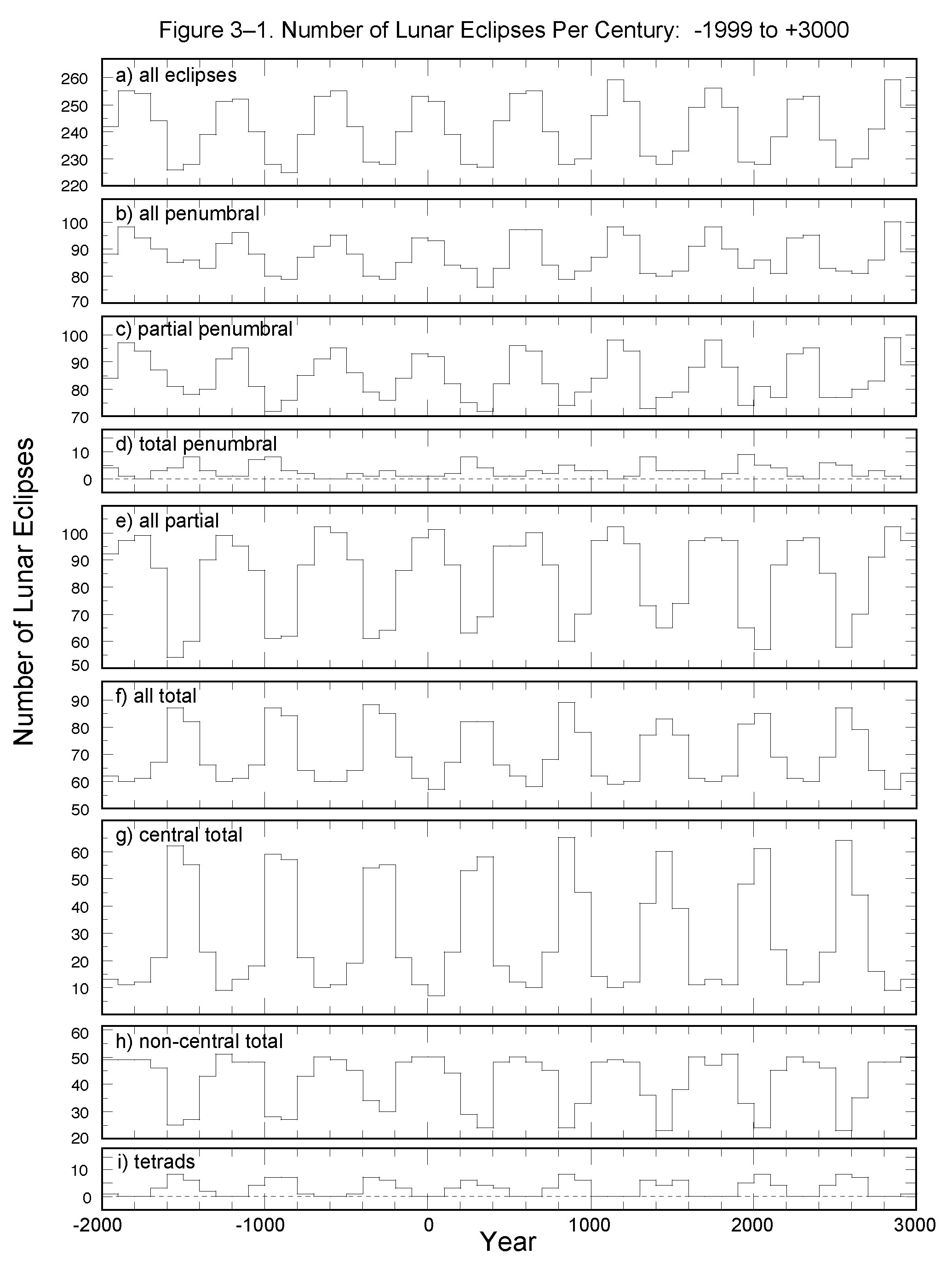
Figure 1 Lunar Eclipse Types by Century
(click for larger figure)
1.3 Distribution of Lunar Eclipse Types by Month
Table 5 summarizes 5,000 years of eclipses by eclipse type in each month of the year. The first value in each column is the number of eclipses of a given type for the corresponding month. The second value, in square brackets [ ], is the number of eclipses divided by the number of days in that month. This normalization allows direct comparison of eclipse frequencies in different months.
A brief examination of the normalized values in the column “Number of All Lunar Eclipses” shows that eclipses are equally distributed around the year. The same holds true for partial eclipses; however, the columns for penumbral and total eclipses reveal something interesting. Penumbral eclipses are about 6% more likely during the period of December– January–February compared to the months June–July–August. This effect is attributed to Earth’s elliptical orbit. Earth currently reaches perihelion in early January and aphelion in early July. Consequently, the Sun’s apparent diameter varies from 1,952 to 1,887 arcsec between perihelion and aphelion. The Sun’s larger apparent diameter at perihelion makes Earth’s penumbral shadow larger so penumbral eclipses are more frequent at that time.
The opposite argument holds true for total eclipses that are about 4% more likely during the period April to August, compared to the months November to February. In this case, the Sun’s smaller apparent size around aphelion increases the diameter of Earth’s umbral shadow so the frequency of total eclipses is slightly higher at that time.
| Table 5. Lunar Eclipse Types by Month: –1999 to +3000 (2000 BCE to 3000 CE) |
||||
| Month | Number of All Eclipses |
Number of Penumbral Eclipses |
Number of Partial Eclipses |
Number of Total Eclipses |
| January | 1027 [33.1] | 379 [12.2] | 352 [11.4] | 296 [ 9.5] |
| February | 936 [33.4] | 343 [12.2] | 333 [11.9] | 260 [ 9.3] |
| March | 1028 [33.2] | 376 [12.1] | 361 [11.6] | 291 [ 9.4] |
| April | 986 [32.9] | 354 [11.8] | 342 [11.4] | 290 [ 9.7] |
| May | 1025 [33.1] | 370 [11.9] | 358 [11.5] | 297 [ 9.6] |
| June | 992 [33.1] | 351 [11.7] | 347 [11.6] | 294 [ 9.8] |
| July | 1025 [33.1] | 368 [11.9] | 356 [11.5] | 301 [ 9.7] |
| August | 1015 [32.7] | 361 [11.6] | 355 [11.5] | 299 [ 9.6] |
| September | 990 [33.0] | 364 [12.1] | 341 [11.4] | 285 [ 9.5] |
| October | 1023 [33.0] | 377 [12.2] | 356 [11.5] | 290 [ 9.4] |
| November | 993 [33.1] | 350 [11.7] | 357 [11.9] | 286 [ 9.5] |
| December | 1024 [33.0] | 385 [12.4] | 349 [11.3] | 290 [ 9.4] |
1.4 Lunar Eclipse Frequency and the Calendar Year
There are 2 to 5 lunar eclipses in every calendar year. Table 6 shows the distribution in the number of eclipses per year for the 5,000 years covered in the Canon of Lunar Eclipses.
| Table 6: Number of Lunar Eclipses per Year –1999 to +3000 (2000 BCE to 3000 CE) |
||
| Number of Eclipses per Year |
Number Years |
Percent |
| 2 | 3,541 | 70.8% |
| 3 | 887 | 17.7% |
| 4 | 539 | 10.8% |
| 5 | 33 | 0.7% |
When two eclipses occur in one calendar year, they can be in any combination of N, P, or T (penumbral, partial, or total, respectively). Figure 7 lists the frequency of each eclipse combination, along with five recent years when the combination occurs. The table makes no distinction in the order of any two eclipses. For example, the eclipse combination PT includes all years where the order is either PT or TP.
Over 71% of all years containing two eclipses are composed of the combinations PP (34.2%) or TT (37.2%). The NT pair is the rarest combination with only six instances, all within the first two millennia of the Canon of Lunar Eclipses, and with five of the six involving a total penumbral eclipse.
| Table 7: Two Lunar Eclipses in One Year –1999 to +3000 (2000 BCE to 3000 CE) |
|||
| Eclipse Combinations a |
Number Years |
Percent | Examples (Years) b |
| NN | 116 | 3.3% | …, 1987, 2016, 2042, 2045, 2053, … |
| NP | 373 | 10.5% | …, 1999, 2005, 2006, 2012, 2017, … |
| NT | 6 | 0.2% | [–1989, –1971, –1423, –1403, –1385, –0186] |
| PP | 1211 | 34.2% | …, 1980, 2039, 2041, 2046, 2057, … |
| PT | 516 | 14.6% | …, 1997, 2008, 2010, 2019, 2021, … |
| TT | 1319 | 37.2% | …, 2003, 2007, 2011, 2014, 2015, … |
-
a - N = Penumbral, P = Partial, and T = Total.
b - When years are surrounded by square brackets [ ], there are no other examples outside this range.
When three eclipses occur in one calendar year, there are nine possible combinations of N, P, or T. Figure 8 lists the frequency of each eclipse combination along with five recent years when each combination occurs. The table makes no distinction in the order of eclipses in any combination. For example, the eclipse combination NPT includes all years where the order is NPT, NTP, PNT, PTN, TPN, and TNP. The rarest combinations–NNT and NTT–each occurs six times or less in the five-millennium span of this work. Interestingly, no PPP combinations occur.
| Table 8: Three Lunar Eclipses in One Year –1999 to +3000 (2000 BCE to 3000 CE) |
|||
| Eclipse Combinations a |
Number Years |
Percent | Recent Examples (Years) b |
| NNN | 382 | 43.1% | …, 2002, 2027, 2031, 2049, 2060, … |
| NNP | 159 | 17.9% | …, 1958, 2013, 2147, 2168, 2186, … |
| NNT | 4 | 0.5% | [–1991, –1405, –0168, 0418] |
| NPP | 158 | 17.8% | …, 1871, 2075, 2140, 2151, 2169, … |
| NPT | 27 | 3.0% | …, 1963, 2001, 2048, 2066, 2504, … |
| NTT | 6 | 0.7% | [–1953, –1432, –1367, –0846, 0977, 2466] |
| PPT | 51 | 5.7% | …, 1898, 2028, 2113, 2178, 2531, … |
| PTT | 75 | 8.5% | …, 1852, 2094, 2159, 2224, 2243, … |
| TTT | 25 | 2.8% | …, 1917, 1982, 2485, 2550, 2615] |
-
a - N = Penumbral, P = Partial, and T = Total.
b - When a year is bounded by a square bracket “[” or “]”, there are no other examples beyond that year.
When four eclipses occur in one calendar year, there are three possible combinations of eclipse types N, P, and T. Figure 9 lists the frequency of each eclipse combination along with five recent years when each combination occurs. The table makes no distinction in the order of eclipses in the seven combinations. The rarest combination NNPP occurs just 32 times.
| Table 9: Four Lunar Eclipses in One Year –1999 to +3000 (2000 BCE to 3000 CE) |
|||
| Eclipse Combinations a |
Number Years |
Percent | Recent Examples (Years) b |
| NNNN | 390 | 72.4% | …, 1944, 2020, 2038, 2056, 2085, … |
| NNNP | 117 | 21.7% | …, 1991, 2009, 2150, 2197, 2215, … |
| NNPP | 32 | 5.9% | …, 1684, 2205, 2411, 2726, 2819, … |
-
a - N = Penumbral, P = Partial, and T = Total.
b - When a year is bounded by a square bracket “[” or “]”, there are no other examples beyond that year.
The maximum number of five lunar eclipses in one calendar year is quite rare. Over the 5,000-year span of the Canon of Lunar Eclipses, there are only 33 years containing five lunar eclipses. They occur in two possible combinations of eclipse types where four out of the five eclipses are always of type N. The first eclipse of such a quintet always occurs in the first half of January, while the last eclipse falls in the latter half of December. Figure 10 lists the frequency of the two eclipse combinations, along with recent years when each combination occurs. The rarest combination NNNPP (actually either PNPNN or NNPNP) occurred just three times. Once again, the table makes no distinction in the order of eclipses in any combination.
| Table 10: Five Lunar Eclipses in One Year –1999 to +3000 (2000 BCE to 3000 CE) |
|||
| Eclipse Combinations a |
Number Years |
Percent | Recent Examples (Years) b |
| NNNNP | 30 | 90.9% | …, 1879, 2132, 2262, 2400, 2653, … |
| NNNPP | 3 | 9.1% | [0475, 1694, 1749] |
-
a - N = Penumbral, P = Partial, and T = Total.
b - When years are surrounded by square brackets [ ], there are no other examples outside this range.
1.5 Extremes in Eclipse Magnitude – Penumbral Lunar Eclipses
The penumbral eclipse magnitude is defined as the fraction of the Moon’s diameter immersed in Earth’s penumbral shadow. It is a unitless parameter that can be expressed numerically by
Mp = xp/dm, (1)
-
where Mp is the penumbral eclipse magnitude, dm is the apparent diameter of the Moon, and xp is the distance measured from the edge of the penumbral shadow to the edge of the Moon deepest in the penumbra.
The penumbral eclipse magnitude reaches its maximum value at the instant of greatest eclipse. This is the value shown in the figures in the Canon of Lunar Eclipses. A search through the 12,064 eclipses in the Canon of Lunar Eclipses reveals some interesting cases involving extreme values of the penumbral eclipse magnitude.
Seven penumbral eclipses have a maximum magnitude less than 0.0020 (Table 11). These events are all the first or last members in a Saros series. The smallest magnitude was the penumbral eclipse of –0780 Dec 13 with a magnitude of just 0.0004.
| Table 11: Penumbral Lunar Eclipses with Magnitude 0.0020 or Less –1999 to +3000 (2000 BCE to 3000 CE) |
||||
| Date (Dynamical Time) |
Saros | Gamma | Penumbral Magnitude |
Eclipse Duration |
| –0780 Dec 13 | 61 | –1.5529 | 0.0004 | 5.2m |
| –0411 Jan 23 | 27 | 1.5791 | 0.0013 | 11.0m |
| –0331 May 07 | 74 | 1.5502 | 0.0008 | 7.8m |
| –0103 Feb 07 | 80 | 1.5540 | 0.0019 | 12.0m |
| 0859 May 20 | 112 | 1.5700 | 0.0007 | 8.1m |
| 2027 Jul 18 | 110 | –1.5758 | 0.0014 | 11.8m |
| 2791 Feb 11 | 175 | –1.5670 | 0.0006 | 7.4m |
Table 12 lists the nine penumbral eclipses having a maximum magnitude greater than 1.0800. The greatest penumbral eclipse occurred on 1322 Nov 24 with a maximum magnitude of 1.0951. Because the penumbral magnitudes of these eclipses are all greater than 1, they are classified as total penumbral eclipses, i.e., the Moon is completely immersed within the penumbral shadow.
| Table 12: Penumbral Lunar Eclipses with Magnitude 1.0800 or More –1999 to +3000 (2000 BCE to 3000 CE) |
||||
| Date (Dynamical Time) |
Saros | Gamma | Penumbral Magnitude |
Eclipse Duration |
| –1517 Jan 12 | 0 | –0.9901 | 1.0858 | 291.2m |
| –1348 Jan 03 | 32 | 0.9948 | 1.0831 | 294.4m |
| –1058 Oct 29 | 19 | 0.9917 | 1.0860 | 291.6m |
| 0348 Oct 24 | 90 | 0.9890 | 1.0946 | 296.1m |
| 1322 Nov 24 | 95 | 0.9897 | 1.0951 | 296.5m |
| 1340 Dec 04 | 95 | 0.9970 | 1.0820 | 295.1m |
| 1988 Mar 03 | 113 | 0.9885 | 1.0907 | 293.8m |
| 2429 Dec 11 | 132 | –0.9904 | 1.0853 | 290.1m |
| 2732 Apr 02 | 163 | –0.9928 | 1.0814 | 293.2m |
1.6 Extremes in Eclipse Magnitude – Partial Eclipses
The umbral eclipse magnitude is defined as the fraction of the Moon’s diameter immersed in Earth’s umbral shadow. It is a unitless parameter that can be expressed numerically by
Mu = xu/dm, (2)
-
where Mu is the umbral eclipse magnitude, dm is the apparent diameter of the Moon,
and xu is the distance measured from the edge of the umbral shadow to the edge of the Moon deepest in the umbra.
The umbral eclipse magnitude reaches its maximum value at the instant of greatest eclipse. This is the value shown in the figures in the Appendix. A search through the 12,064 eclipses in the Canon of Lunar Eclipses reveals some interesting cases involving extreme values of the umbral eclipse magnitude in partial and total lunar eclipses.
Eleven partial eclipses have a maximum magnitude (at greatest eclipse) less than or equal to 0.0020 (Table 13). The partial eclipse with the smallest magnitude (at greatest eclipse) occurred on 1553 Jul 25 and had a magnitude of just 0.0001.
| Table 13: Partial Lunar Eclipses with Magnitude 0.0020 or Less –1999 to +3000 (2000 BCE to 3000 CE) |
||||
| Date (Dynamical Time) |
Saros | Gamma | Umbral Eclipse Magnitude |
Partial Eclipse Duration |
| –0602 May 03 | 31 | 0.9940 | 0.0015 | 9.7m |
| –0519 May 15 | 32 | –1.0261 | 0.0004 | 4.3m |
| –0292 Mar 27 | 66 | 1.0016 | 0.0010 | 7.5m |
| 1050 Feb 09 | 108 | 0.9861 | 0.0013 | 8.9m |
| 1416 Nov 05 | 97 | 1.0107 | 0.0019 | 9.9m |
| 1430 Sep 02 | 128 | 1.0229 | 0.0008 | 6.3m |
| 1553 Jul 25 | 131 | –1.0253 | 0.0001 | 2.5m |
| 1890 Nov 26 | 114 | –0.9994 | 0.0017 | 9.8m |
| 2157 Feb 24 | 145 | –0.9868 | 0.0005 | 5.6m |
| 2421 Jun 16 | 156 | 1.0225 | 0.0011 | 7.3m |
| 2627 May 22 | 160 | 0.9914 | 0.0011 | 8.0m |
Nine partial eclipses have a maximum magnitude (at greatest eclipse) greater than or equal to 0.9980 (Table 14). The partial eclipse with the largest magnitude (at greatest eclipse) occurred on –1972 Jun 27 with a magnitude of 0.9998.
| Table 14: Partial Lunar Eclipses with Magnitude 0.9980 or More –1999 to +3000 (2000 BCE to 3000 CE) |
||||
| Date (Dynamical Time) |
Saros | Gamma | Umbral Eclipse Magnitude |
Partial Eclipse Duration |
| –1972 Jun 27 | –2 | –0.4505 | 0.9998 | 209.0m |
| –1021 May 16 | 24 | –0.4758 | 0.9986 | 192.6m |
| –0247 Oct 03 | 52 | –0.4532 | 0.9988 | 202.7m |
| 0145 Sep 18 | 78 | 0.4511 | 0.9994 | 205.0m |
| 0274 Apr 08 | 65 | 0.4523 | 0.9993 | 207.1m |
| 0778 Sep 11 | 98 | 0.4670 | 0.9993 | 195.0m |
| 1001 Mar 12 | 87 | 0.4728 | 0.9995 | 191.1m |
| 1165 May 27 | 107 | –0.4727 | 0.9986 | 194.5m |
| 2413 Nov 08 | 152 | 0.4733 | 0.9993 | 189.5m |
1.7 Extremes in Eclipse Magnitude – Total Lunar Eclipses
Twelve total eclipses have a maximum magnitude less than or equal to 1.0020 (Table 15). The smallest magnitude was the total eclipse of 1529 Oct 17 with a value of just 1.0001 (note the upcoming total eclipse of 2015 Apr 04 and its magnitude of 1.0008). Because the Moon’s passage through the umbral shadow is so shallow, these events all have short total phases less than 7 min.
| Table 15: Total Lunar Eclipses with Magnitude 1.0020 or Less –1999 to +3000 (2000 BCE to 3000 CE) |
||||
| Date (Dynamical Time) |
Saros | Gamma | Umbral Eclipse Magnitude |
Total Eclipse Duration |
| –1573 Jan 31 | 18 | 0.4776 | 1.0008 | 4.2m |
| –1338 Jun 09 | 28 | 0.4622 | 1.0012 | 5.5m |
| –0318 Aug 10 | 62 | 0.4474 | 1.0009 | 4.9m |
| –0200 Mar 30 | 48 | –0.4790 | 1.0019 | 6.6m |
| 0767 Apr 19 | 92 | 0.4581 | 1.0002 | 2.4m |
| 0792 Dec 03 | 96 | 0.4413 | 1.0004 | 3.1m |
| 1529 Oct 17 | 109 | 0.4775 | 1.0001 | 1.7m |
| 2015 Apr 04 | 132 | 0.4460 | 1.0008 | 4.7m |
| 2155 Sep 11 | 130 | –0.4752 | 1.0003 | 2.6m |
| 2366 May 25 | 146 | 0.4817 | 1.0007 | 3.9m |
| 2565 Sep 11 | 156 | 0.4700 | 1.0009 | 4.6m |
| 2905 Jun 08 | 164 | 0.4748 | 1.0018 | 6.5m |
Eight total eclipses have a maximum magnitude greater than or equal to 1.8700. Their total phase durations all last 98 to 99 min and gamma values are all close to 0.0 indicating that the Moon passes centrally through the middle of the umbral shadow. These eclipses all take place when the Moon is near perigee–the time when the ratio of the Moon’s to umbra’s diameters is at maximum. The total eclipse with the largest magnitude (1.8821) occurs on 2756 Jun 05.
| Table 16: Total Lunar Eclipses with Magnitude 1.8700 or More –1999 to +3000 (2000 BCE to 3000 CE) |
||||
| Date (Dynamical Time) |
Saros | Gamma | Umbral Eclipse Magnitude |
Total Eclipse Duration |
| –0731 Apr 19 | 39 | –0.0054 | 1.8766 | 99.4m |
| –0630 Nov 06 | 45 | –0.0002 | 1.8703 | 98.3m |
| –0051 Apr 01 | 60 | –0.0009 | 1.8774 | 99.7m |
| 0564 Sep 06 | 85 | 0.0017 | 1.8764 | 98.9m |
| 1092 Apr 24 | 97 | 0.0080 | 1.8702 | 99.3m |
| 1226 Aug 09 | 106 | –0.0021 | 1.8770 | 99.6m |
| 1631 May 15 | 115 | 0.0052 | 1.8721 | 99.8m |
| 2756 Jun 05 | 152 | 0.0018 | 1.8821 | 99.3m |
1.8 Greatest Duration – Penumbral Lunar Eclipses
Nine penumbral eclipses each have durations of 292 min or more. Because the penumbral eclipse magnitude of each of these events is greater than 1, they are all classified as total penumbral eclipses. Each eclipse in Table 17 occurs near lunar apogee and within several weeks of aphelion. Earth’s penumbra is then largest, while the Moon exhibits a small angular diameter and travels relatively slowly, thereby extending the length of the eclipse.
| Table 17: Penumbral Lunar Eclipses with Duration of 292 min or More –1999 to +3000 (2000 BCE to 3000 CE) |
||||
| Date (Dynamical Time) |
Saros | Gamma | Penumbral Eclipse Magnitude |
Penumbral Eclipse Duration |
| –1367 Dec 23 | 32 | 1.0089 | 1.0588 | 292.2m |
| –1348 Jan 03 | 32 | 0.9948 | 1.0831 | 294.4m |
| 0348 Oct 24 | 90 | 0.9890 | 1.0946 | 296.1m |
| 1322 Nov 24 | 95 | 0.9897 | 1.0951 | 296.5m |
| 1340 Dec 04 | 95 | 0.9970 | 1.0820 | 295.1m |
| 1358 Dec 16 | 95 | 1.0039 | 1.0693 | 293.6m |
| 1376 Dec 26 | 95 | 1.0104 | 1.0569 | 292.1m |
| 1988 Mar 03 | 113 | 0.9885 | 1.0907 | 293.8m |
| 2732 Apr 02 | 163 | –0.9928 | 1.0814 | 293.2m |
1.9 Greatest Duration – Partial Lunar Eclipses
Seven partial eclipses have durations of 209 min or more. All of these events occur with the Moon close to apogee so its slow trajectory through the umbra tends to prolong the partial phase.
| Table 18: Partial Lunar Eclipses with Duration of 209 min or More –1999 to +3000 (2000 BCE to 3000 CE) |
||||
| Date (Dynamical Time) |
Saros | Gamma | Umbral Eclipse Magnitude |
Partial Eclipse Duration |
| –1274 Jun 21 | 19 | 0.4611 | 0.9768 | 209.3m |
| –1133 May 24 | 22 | –0.4592 | 0.9814 | 209.6m |
| –0764 Jan 26 | 31 | 0.4540 | 0.9771 | 209.1m |
| –0387 Oct 20 | 59 | –0.4458 | 0.9908 | 209.3m |
| 0303 Sep 12 | 71 | 0.4510 | 0.9864 | 209.6m |
| 1382 Sep 23 | 117 | –0.4458 | 0.9977 | 209.6m |
| 2669 Feb 08 | 144 | –0.4424 | 0.9951 | 210.0m |
1.10 Greatest Duration – Total Lunar Eclipses
Eighteen total eclipses have durations greater than or equal to 106 min. The most recent one was 2000 Jul 16, while the next is 2123 Jun 09. All of these eclipses occur near aphelion and with the Moon close to apogee. Consequently, the Moon has a small angular diameter coupled with a relatively slow orbital motion with respect to the umbra. Furthermore, the umbral shadow is largest when Earth is at aphelion. Such conditions prolong the Moon’s passage through the umbra to produce long total lunar eclipses (Meeus, 2002).
Earth’s tropical longitude of perihelion is currently increasing by 1.72° per century. This means that the date of aphelion occurred about 17 days earlier for each 1000 years backwards from the present. This too is reflected in the dates seen in Table 19.
| Table 19: Total Lunar Eclipses with Duration of 106 min or More –1999 to +3000 (2000 BCE to 3000 CE) |
||||
| Date (Dynamical Time) |
Saros | Gamma | Umbral Eclipse Magnitude |
Total Eclipse Duration |
| –1921 Apr 07 | 1 | 0.0302 | 1.7681 | 106.2m |
| –1646 Jun 24 | 13 | 0.0164 | 1.7946 | 106.3m |
| –1505 May 27 | 16 | –0.0171 | 1.7948 | 106.5m |
| –1364 Apr 28 | 19 | 0.0187 | 1.7910 | 106.4m |
| –0380 Jun 06 | 53 | –0.0308 | 1.7703 | 106.2m |
| –0239 May 09 | 56 | 0.0301 | 1.7713 | 106.1m |
| –0098 Apr 11 | 59 | –0.0016 | 1.8212 | 106.1m |
| 0054 Aug 07 | 68 | –0.0147 | 1.7924 | 106.2m |
| 0177 Jun 28 | 71 | –0.0198 | 1.7874 | 106.5m |
| 0318 May 31 | 74 | 0.0160 | 1.7951 | 106.6m |
| 0459 May 03 | 77 | 0.0033 | 1.8167 | 106.5m |
| 1443 Jun 12 | 111 | –0.0098 | 1.8097 | 106.2m |
| 1584 May 24 | 114 | –0.0065 | 1.8145 | 106.1m |
| 1859 Aug 13 | 126 | 0.0038 | 1.8148 | 106.5m |
| 2000 Jul 16 | 129 | 0.0302 | 1.7684 | 106.4m |
| 2123 Jun 09 | 132 | 0.0406 | 1.7487 | 106.1m |
| 2141 Jun 19 | 132 | –0.0446 | 1.7415 | 106.1m |
| 2264 May 12 | 135 | 0.0121 | 1.7979 | 106.2m |
1.11 Total Penumbral Lunar Eclipses
During most penumbral eclipses, only part of the Moon passes through Earth’s penumbral shadow. However, it is also possible to have a penumbral eclipse in which the entire Moon passes completely within Earth’s penumbral shadow without entering the inner umbral shadow. The geocentric apparent diameter of the Moon ranges from an extreme minimum of 1763.0 arcsec (apogee) to an extreme maximum of 2011.8 arcsec (perigee). The penumbral annulus formed by the zone between the outer edges of the penumbra and umbra also undergoes extremes ranging from 1887.7 arcsec (aphelion) to 1951.9 arcsec (perihelion). From these values, it is apparent that the Moon cannot fit entirely within the penumbral annulus when it is near perigee (Meeus, 1997). As a consequence of the restrictive geometry and conditions, total penumbral eclipses are quite rare and account for just 3.2%, or 141 out of 4378 penumbral eclipses in the Canon of Lunar Eclipses. Table 20 lists the dates of all 141 total penumbral eclipses.
The frequency of total penumbra䁬 eclipse varies considerably with time. If the 5,000-year period covered by the Canon of Lunar Eclipses is divided into 100-year intervals, the number of total penumbral eclipses per century varies from 0 to a maximum of 9 (Table 4). For instance, the number of total penumbral eclipses in centuries beginning in 1701, 1801, and 1901 are 0, 2, and 9, respectively. The number of total penumbral eclipses appears to be correlated with the number of total eclipses, as well as the number of tetrads per century, and inversely correlated with the overall number of all lunar eclipses per century. When a century has a relatively large number of lunar eclipses, it has fewer total lunar eclipses and few or no total penumbral lunar eclipses or tetrads (Figure 1).
| Table 20: Total Penumbral Lunar Eclipses –1999 to +3000 (2000 BCE to 3000 CE) |
|||||
| -1989 Dec 01 | -1142 Jun 02 | -0274 Oct 02 | 0682 Apr 27 | 1455 Oct 25 | 2103 Jan 23 |
| -1981 Jul 07 | -1058 Oct 29 | -0263 Aug 31 | 0711 Oct 01 | 1496 Jul 25 | 2121 Feb 02 |
| -1971 Dec 12 | -1040 Nov 08 | -0205 Jan 26 | 0729 Oct 11 | 1502 Apr 22 | 2128 Mar 16 |
| -1953 Dec 23 | -1022 Nov 19 | -0186 Jun 22 | 0805 Mar 19 | 1513 Sep 15 | 2139 Feb 13 |
| -1840 Jun 08 | -1018 Mar 14 | -0045 May 25 | 0816 Aug 11 | 1542 Aug 25 | 2222 Aug 23 |
| -1699 May 11 | -1007 Aug 07 | 0096 Apr 26 | 0822 May 09 | 1607 Mar 13 | 2429 Dec 11 |
| -1669 Sep 05 | -1004 Nov 30 | 0154 Sep 09 | 0823 Sep 24 | 1637 Jul 07 | 2447 Dec 22 |
| -1604 Mar 13 | -1001 May 05 | 0197 Nov 12 | 0862 Sep 12 | 1665 Jul 27 | 2458 May 28 |
| -1575 Aug 17 | -0986 Dec 11 | 0215 Nov 24 | 0945 Mar 31 | 1806 Jun 30 | 2466 Jan 01 |
| -1564 Jul 16 | -0968 Dec 21 | 0219 Mar 18 | 0974 Sep 04 | 1900 Jun 13 | 2484 Jan 13 |
| -1558 Apr 13 | -0964 Oct 10 | 0233 Dec 04 | 0996 Jan 08 | 1901 May 03 | 2498 Sep 30 |
| -1517 Jan 12 | -0949 Jan 02 | 0248 Aug 21 | 1014 Jan 19 | 1908 Dec 07 | 2502 Jan 24 |
| -1499 Jan 22 | -0946 Oct 21 | 0251 Dec 15 | 1032 Jan 30 | 1926 Dec 19 | 2520 Feb 04 |
| -1457 Oct 30 | -0943 Sep 17 | 0265 Apr 18 | 1097 Jul 27 | 1944 Dec 29 | 2523 Nov 24 |
| -1452 Jul 08 | -0931 Jan 12 | 0269 Dec 26 | 1221 May 08 | 1948 Oct 18 | 2538 Feb 15 |
| -1439 Nov 10 | -0925 Sep 29 | 0288 Jan 06 | 1322 Nov 24 | 1963 Jan 09 | 2562 Nov 12 |
| -1435 Mar 05 | -0860 Apr 06 | 0312 Oct 02 | 1340 Dec 04 | 1981 Jan 20 | 2656 Oct 25 |
| -1421 Nov 21 | -0838 Jul 29 | 0330 Oct 13 | 1344 Mar 29 | 1988 Mar 03 | 2714 Mar 23 |
| -1406 Aug 09 | -0831 Sep 10 | 0348 Oct 24 | 1358 Dec 16 | 1999 Jan 31 | 2732 Apr 02 |
| -1403 Dec 01 | -0755 Feb 15 | 0388 Mar 09 | 1373 Sep 02 | 2006 Mar 14 | 2761 Sep 06 |
| -1385 Dec 13 | -0726 Jul 22 | 0417 Aug 13 | 1376 Dec 26 | 2053 Aug 29 | 2885 Jun 18 |
| -1367 Dec 23 | -0461 Apr 05 | 0512 Jun 15 | 1390 Apr 29 | 2070 Apr 25 | |
| -1348 Jan 03 | -0432 Sep 08 | 0653 May 18 | 1395 Jan 06 | 2082 Aug 08 | |
| -1283 Jun 30 | -0356 Feb 14 | 0681 Jun 07 | 1413 Jan 17 | 2099 Sep 29 | |
1.12 Lunar Eclipse Duos
A duo is a pair of eclipses separated by one lunation (synodic month). Of the 12,064 eclipses in the Canon of Lunar Eclipses, 3,054 eclipses (25.3%) belong to a duo. One eclipse of a duo always passes north of Earth’s shadow axis, while the other eclipse passes to the south. In most cases, both eclipses in a duo are penumbral eclipses; however, there are 51 instances (3.3% of duos) in the Canon where one eclipse is penumbral and the other is partial. In each of these pairs, the penumbral magnitude of the penumbral eclipse is quite small, as is the umbral magnitude of the partial eclipse. The dates and eclipse combinations of all lunar eclipse duos are listed in Table 21.
| Table 21: Lunar Eclipse Duos of Two Types –1999 to +3000 (2000 BCE to 3000 CE) |
||||
| –1952 May-Jun - NP | –0668 May-Jun - NP | 0475 Jun-Jul - NP | 1296 Apr-May - NP | 2288 Jul-Aug - PN |
| –1811 Apr-May - NP | –0527 Apr-May - NP | 0483 Jul-Aug - PN | 1427 Apr-May - PN | 2411 Jun-Jul - PN |
| –1774 May-May - PN | –0519 May-Jun - PN | 0606 May-Jun - PN | 1430 Aug-Sep - NP | 2429 Jun-Jul - PN |
| –1670 Mar-Apr - NP | –0252 Jul-Jul - NP | 0624 Jun-Jul - PN | 1553 Jun-Jul - NP | 2552 May-Jun - PN |
| –1492 Mar-Apr - PN | –0111 Jun-Jul - NP | 0747 Apr-May - PN | 1608 Jul-Aug - PN | 2819 Jun-Jul - NP |
| –1358 Jun-Jul - PN | –0074 Jun-Jul - PN | 0888 Mar-Apr - PN | 1694 Jun-Jul - NP | 2827 Jul-Aug - PN |
| –1217 May-Jun - PN | 0030 May-Jun - NP | 0891 Jul-Aug - NP | 1749 Jun-Jul - PN | 2960 Jun-Jun - NP |
| –1076 Apr-May - PN | 0067 May-Jun - PN | 1014 Jun-Jul - NP | 1835 May-Jun - NP | |
| –0935 Mar-Apr - PN | 0153 Mar-Apr - NP | 1022 Jul-Aug - PN | 1958 Apr-May - NP | |
| –0932 Jul-Aug - NP | 0208 Apr-May - PN | 1155 May-Jun - NP | 2013 Apr-May - PN | |
| –0809 Jun-Jul - NP | 0428 Jun-Jul - NP | 1163 Jun-Jul - PN | 2147 Aug-Sep - PN | |
1.13 Lunar Eclipses Duos in One Calendar Month
There are 57 instances where both members of an eclipse duo occur in one calendar month. In most cases, both eclipses in the duos are penumbral. In three instances, the duo consists of the NP combination (–1774 May, –0252 Jul, and 2960 Jun). The year and month of each duo appears in Table 22.
| Table 22: Two Lunar Eclipses in One Calendar Month –1999 to +3000 (2000 BCE to 3000 CE) |
|||||
| -1883 Sep | -1033 Jan | -0078 Mar | 0768 Sep | 1694 Dec | 2566 Aug |
| -1861 Jul | -0765 Aug | 0019 Dec | 0790 Jul | 1705 Nov | 2577 Jul |
| -1807 Aug | -0686 May | 0074 Jan | 0877 May | 1716 Oct | 2838 Jan |
| -1796 Jul | -0675 Apr | 0269 Jul | 1116 Jan | 1817 May | 2848 Dec |
| -1785 Jun | -0599 Mar | 0291 May | 1126 Dec | 1904 Mar | 2957 Aug |
| -1785 Jun | -0512 Jan | 0356 May | 1213 Oct | 2172 Oct | 2960 Jun |
| -1706 Mar | -0502 Dec | 0367 Apr | 1289 Sep | 2208 May | 2968 Jul |
| -1286 Aug | -0447 Jan | 0443 Mar | 1300 Aug | 2284 Apr | |
| -1275 Jul | -0252 Jul | 0595 Jan | 1311 Jul | 2295 Mar | |
| -1185 Mar | -0165 May | 0605 Dec | 1376 Jul | 2382 Jan | |
1.14 January–March Lunar Eclipse Duos
The mean length of one synodic month is 29.5306 days (in year 2000). Because this is longer than the month of February, it is possible to have one member of an eclipse duo in January followed by the second in March. There are six instances of such a rare January/March duo in the Canon of Lunar Eclipses: –1109, –0523, –0002, 1915, 2306, and 2371. In all cases, both eclipses in the duos are penumbral.
1.15 Total Lunar Eclipse Multiplets
A total lunar eclipse is usually preceded or succeeded by at least one other total lunar eclipse. Of the 3479 total eclipses in the Canon of Lunar Eclipses, 1798 of them (51.7%) are part of a doublet. Another 1023 eclipses (29.4%) belong to a triplet. Finally, 568 total eclipses (16.3%) are part of a quadruplet known as a tetrad. In comparison, only 90 total eclipses (2.6%) occur as solitary singlets.
A key feature of total lunar eclipse multiplets is that the individual members are always separated by six lunations. A summary of the muliplet statistics appears in Table 23.
| Table 23: Total Lunar Eclipse Multiplets –1999 to +3000 (2000 BCE to 3000 CE) |
|||||
| Total Eclipse Multiplets |
Number of Eclipses Per Multiplet |
Number of Multiplets |
Number of Total Eclipses |
Percent of Total Eclipses |
Recent Examples |
| All Total Eclipses | - | - | 3479 | 100.0% | - |
| Singlet | 1 | 90 | 90 | 2.6% | 1997 Sep 16; 2021 May 26 |
| Doublet | 2 | 899 | 1798 | 51.7% | 1978; 1996; 2022; 2040 |
| Triplet | 3 | 341 | 1023 | 29.4% | 2007 to 2008; 2010 to 2011 |
| Tetrad | 4 | 142 | 568 | 16.3% | 2014 to 2015; 2032 to 2033 |
1.16 Lunar Eclipse Tetrads
When four consecutive lunar eclipses are all total, the group is termed a tetrad. As discussed previously, 16.3% (568 out of 3479) of all total eclipses are members of a tetrad. These 142 groupings of total eclipses occur because of the eccentricity of Earth’s orbit in conjunction with the timing of eclipse seasons (Section 1.18). During the first 1,000 years of the Canon of Lunar Eclipses, the first eclipse of every tetrad occurs sometime from December to May. In later millennia, the first eclipse date occurs later in the year because of precession–during the 3rd Millennium, the period for the first date extends from February to July. For a detailed description of tetrad geometry and an explanation of why tetrads happen, see Meeus (2004b).
Italian astronomer Giovanni Schiaparelli first pointed out that the frequency of tetrads is variable over time. He noticed that tetrads were relatively plentiful during one 300-year interval, while none occurred during the next 300 years. For example, there are no tetrads from 1582 to 1908, but 17 tetrads occur during the following 2 1⁄2 centuries from 1909 to 2156. This can be seen graphically in Figure 1i. The 565-year period of the tetrad “seasons” is tied to the slowly decreasing eccentricity of Earth’s orbit. Consequently, the tetrad period is gradually decreasing (Hughes, 2004). In the distant future, when Earth’s eccentricity is 0, tetrads will no longer be possible.
The umbral magnitudes of the total eclipses making up a tetrad are all relatively small. For the 300-year period 1901 to 2200, the largest umbral magnitude of a tetrad eclipse is 1.4251 on 1949 Apr 13. For comparison, some other total eclipses during this period are much deeper. Two examples are the total eclipses of 2000 Jul 16 and 2029 Jun 26 with umbral magnitudes of 1.7684 and 1.8436, respectively.
Table 24 lists the date of the first total lunar eclipse in each of the 142 tetrads in the Canon of Lunar Eclipses.
| Table 24: Date of First Eclipse in Lunar Eclipse Tetrads –1999 to +3000 (2000 BCE to 3000 CE) |
|||||
| -1991 Dec 22 | -0999 Mar 14 | -0283 Mar 18 | 0766 Apr 29 | 1457 Mar 11 | 2137 Mar 07 |
| -1661 Apr 12 | -0981 Mar 25 | -0272 Feb 16 | 0784 May 09 | 1475 Mar 22 | 2155 Mar 19 |
| -1643 Apr 22 | -0963 Apr 04 | -0243 Jan 26 | 0795 Apr 09 | 1493 Apr 02 | 2448 Jun 17 |
| -1625 May 04 | -0945 Apr 16 | -0225 Feb 06 | 0802 May 21 | 1504 Mar 01 | 2466 Jun 28 |
| -1596 Apr 13 | -0923 Feb 12 | -0207 Feb 16 | 0813 Apr 19 | 1515 Jan 30 | 2477 May 28 |
| -1585 Mar 13 | -0916 Mar 26 | -0189 Feb 28 | 0824 Mar 18 | 1522 Mar 12 | 2495 Jun 08 |
| -1578 Apr 24 | -0905 Feb 24 | -0168 Dec 27 | 0842 Mar 30 | 1533 Feb 09 | 2506 May 08 |
| -1574 Feb 10 | -0887 Mar 06 | -0149 Jan 07 | 0860 Apr 09 | 1562 Jan 20 | 2524 May 19 |
| -1567 Mar 24 | -0876 Feb 03 | 0162 Apr 17 | 0878 Apr 20 | 1580 Jan 31 | 2542 May 30 |
| -1556 Feb 21 | -0869 Mar 17 | 0180 Apr 27 | 0889 Mar 21 | 1909 Jun 04 | 2564 Mar 29 |
| -1538 Mar 04 | -0858 Feb 14 | 0198 May 08 | 0900 Feb 18 | 1927 Jun 15 | 2571 May 11 |
| -1520 Mar 14 | -0847 Jan 14 | 0227 Apr 19 | 0918 Feb 28 | 1949 Apr 13 | 2582 Apr 09 |
| -1473 Mar 06 | -0840 Feb 25 | 0238 Mar 18 | 0936 Mar 11 | 1967 Apr 24 | 2589 May 21 |
| -1462 Feb 02 | -0829 Jan 25 | 0245 Apr 29 | 0947 Feb 08 | 1985 May 04 | 2600 Apr 20 |
| -1444 Feb 13 | -0782 Jan 15 | 0256 Mar 28 | 0965 Feb 18 | 2003 May 16 | 2611 Mar 20 |
| -1433 Jan 13 | -0453 May 06 | 0267 Feb 26 | 0976 Jan 19 | 2014 Apr 15 | 2618 May 01 |
| -1415 Jan 23 | -0377 Apr 06 | 0285 Mar 08 | 0994 Jan 30 | 2032 Apr 25 | 2629 Mar 31 |
| -1405 Dec 24 | -0359 Apr 17 | 0332 Feb 28 | 1305 May 09 | 2043 Mar 25 | 2640 Feb 29 |
| -1386 Jan 04 | -0341 Apr 28 | 0350 Mar 10 | 1323 May 21 | 2050 May 06 | 2647 Apr 11 |
| -1368 Jan 15 | -0330 Mar 28 | 0361 Feb 06 | 1341 May 31 | 2061 Apr 04 | 2658 Mar 11 |
| -1057 Apr 24 | -0319 Feb 24 | 0390 Jan 17 | 1352 Apr 30 | 2072 Mar 04 | 2676 Mar 22 |
| -1039 May 05 | -0312 Apr 07 | 0408 Jan 29 | 1370 May 11 | 2090 Mar 15 | 2987 Jul 02 |
| -1028 Apr 03 | -0301 Mar 07 | 0437 Jan 08 | 1399 Apr 20 | 2101 Feb 14 | |
| -1010 Apr 14 | -0290 Feb 04 | 0455 Jan 19 | 1428 Mar 31 | 2119 Feb 25 | |
1.17 Lunar Eclipses on February 29
There are six instances of a lunar eclipse occurring on February 29. Two eclipses are penumbral, two are partial, and two are total. A list of eclipses on February 29 with physical parameters appears in Table 25.
| Table 25: Lunar Eclipses on February 29 –1999 to +3000 (2000 BCE to 3000 CE) |
||||
| Date (Dynamical Time) |
Eclipse Type |
Saros | Gamma | Umbral Eclipse Magnitude |
| –0664 Feb 29 | N | 22 | –1.3596 | 0.3819a |
| –0588 Feb 29 | N | 62 | 1.4929 | 0.1363a |
| –0124 Feb 29 | P | 50 | –0.5634 | 0.8114 |
| 1420 Feb 29 | P | 94 | –0.9205 | 0.1614 |
| 2268 Feb 29 | T– | 137 | –0.1142 | 1.6602 |
| 2640 Feb 29 | T | 143 | 0.3353 | 1.2478 |
-
a - Penumbral Eclipse Magnitude
1.18 Eclipse Seasons
The 5.1° inclination of the lunar orbit around Earth means that the Moon’s orbit crosses the ecliptic at two points or nodes. If Full Moon takes place within about 16° of a node [2], then a lunar eclipse will be visible from a portion of Earth.
The Sun makes one complete circuit of the ecliptic in 365.24 days, so its average angular velocity is 0.99° per day. At this rate, it takes 34.5 days for Earth’s umbral and penumbral shadows to cross the 34° wide eclipse zone centered on each node. Because the Moon’s orbit with respect to the Sun has a mean duration of 29.53 days, there will always be one, and possibly two, lunar eclipses during each 34.5-day interval when the Sun (and Earth’s shadows) pass through the nodal eclipse zones. These time periods are called eclipse seasons.
The mid-point of each eclipse season is separated by 173.3 days because this is the mean time for the Sun to travel from one node to the next. The period is a little less than half a calendar year because the lunar nodes slowly regress westward by 19.3° per year.
Footnotes
[2] The actual value ranges from 15.2° to 16.8° because of the eccentricity of the Moon's and Earth's orbits. If a lunar eclipse occurs within 9.4° to 11.0° of a node, the eclipse will be partial. A lunar eclipse within 4.2° to 5.0°of a node will be total.
1.19 Quincena
The mean time interval between New Moon and Full Moon is 14.77 days. This is less than half the duration of an eclipse season. As a consequence, the same Sun–node alignment geometry responsible for producing a lunar eclipse always results in a complementary solar eclipse within a fortnight. The solar eclipse may either precede or succeed the lunar eclipse. In either case, the pair of eclipses is referred to here as a quincena. The Quincena Solar Eclipse (QSE) parameter identifies the type of the solar eclipse and whether it precedes or succeeds a particular lunar eclipse. There are four types of solar eclipses:
- p = partial solar eclipse
(Moon’s penumbral shadow traverses Earth; umbral/antumbral shadow completely misses Earth) - a = annular solar eclipse
(Moon’s antumbral shadow traverses Earth; Moon is too far from Earth to completely cover the Sun) - t = total solar eclipse
(Moon’sumbral shadow traverses Earth; Moon is close enough to Earth to completely cover the Sun) - h = hybrid solar eclipse
(Moon’s umbral and antumbral shadows traverse different parts of Earth; eclipse appears either total or annular along different sections of its path–hybrid eclipses are also known as annular-total eclipses)
The QSE is a two character string consisting of one or more of the above solar eclipse types. The first character in the QSE identifies a solar eclipse preceding a lunar eclipse while the second character identifies a solar eclipse succeeding a lunar eclipse. In most instances, one of the two characters is “–” indicating a single solar eclipse either precedes or succeeds the lunar eclipse. On rare occasions, a double quincena occurs in which a lunar eclipse is both preceded and succeeded by solar eclipses.
1.20 Quincena Combinations with Total Lunar Eclipses
A total lunar eclipse can be preceded or succeeded by a total solar eclipse (7.7%), an annular solar eclipse (10.2%), a hybrid solar eclipse (0.4%), or a partial solar eclipse (42.5%). Double quincenas (a lunar eclipse is both preceded and succeeded by a solar eclipse) occur with a frequency of 39.1% and usually consist of two partial solar eclipses (38.7%). In rare instances, a double quincena consists of a total and a partial solar eclipse (0.4%). A complete list of all QSE combinations with total lunar eclipses appears in Table 26. The most recent years when each quincena combination occurs are given in the last column.
| Table 26: Quincena Combinations with Total Lunar Eclipses –1999 to +3000 (2000 BCE to 3000 CE) |
||||
| Quincena Solar Eclipse |
QSE | Number | Percent | Recent Examples (Years) a |
| – total | –t | 127 | 3.7% | …, 1985, 2003, 2043, 2061, 2072,… |
| total – | t– | 139 | 4.0% | …, 1957, 1968, 2015, 2033, 2044,… |
| – annular | –a | 178 | 5.1% | …, 1891, 2003, 2014, 2021, 2032,… |
| annular – | a– | 178 | 5.1% | …, 1990, 2008, 2026, 2044, 2102,… |
| – hybrid | –h | 12 | 0.3% | …, 1627, 1645, 1768, 1909, 2050,… |
| hybrid – | h– | 5 | 0.1% | [ –1989, –1848, –1642, 0163, 1986] |
| – partial | –p | 730 | 21.0% | …, 2000, 2007, 2010, 2014, 2018,… |
| partial – | p– | 749 | 21.5% | …, 2001, 2004, 2011, 2015, 2019,… |
| total – partial | tp | 8 | 0.2% | …, –0434, –0159, 1248, 1928, 2912] |
| partial – total | pt | 6 | 0.2% | [ –1310, –1169, –1028, –0026, 2195, 2459] |
| partial – partial | pp | 1347 | 38.7% | …, 1982, 2000, 2011, 2018, 2029,… |
-
a - When a year is bounded by a square bracket “[” or “]”, there are no other examples beyond that year.
1.21 Quincena Combinations with Partial Lunar Eclipses
A partial lunar eclipse can be preceded or succeeded by a total solar eclipse (37.6%), an annular solar eclipse (55.1%), or a hybrid solar eclipse (6.9%). In rare instances, a partial lunar eclipse can be followed by a partial solar eclipse (0.3%). Double quincenas do not occur with partial lunar eclipses. A list of quincena solar eclipse combinations with partial lunar eclipses appears in Table 27. The most recent years when each quincena combination occurs are given in the last column.
| Table 27: Quincena Combinations with Partial Lunar Eclipses –1999 to +3000 (2000 BCE to 3000 CE) |
||||
| Quincena Solar Eclipse |
QSE | Number | Percent | Recent Examples (Years) a |
| – total | –t | 782 | 18.6% | …, 1992, 1999, 2010, 2017, 2021,… |
| total – | t– | 801 | 19.0% | …, 2001, 2008, 2019, 2026, 2037,… |
| – annular | –a | 1149 | 27.3% | …, 1995, 2006, 2009, 2013, 2024,… |
| annular – | a– | 1171 | 27.8% | …, 1994, 2005, 2012, 2023, 2030,… |
| – hybrid | –h | 167 | 4.0% | …, 1912, 1930, 2209, 2350, 2368,… |
| hybrid – | h– | 124 | 2.9% | …, 1827, 1845, 2164, 2182, 2323,… |
| – partial | –p | 13 | 0.3% | …, –0754, –0196, 2086, 2607, 2625,… |
-
a - When a year is bounded by a square bracket “[” or “]”, there are no other examples beyond that year.
1.22 Quincena Combinations with Penumbral Lunar Eclipses
A penumbral lunar eclipse can be preceded or succeeded by a total solar eclipse (39.5%), an annular solar eclipse (51.9%), or a hybrid solar eclipse (8.7%). There are no instances of a quincena involving a partial solar and a penumbral lunar eclipse, nor are there any double quincenas in the Canon of Lunar Eclipses. A list of quincena solar eclipse combinations with penumbral lunar eclipses appears in Table 28. The most recent years when each quincena combination occurs are given in the last column.
| Table 28: Quincena Combinations with Penumbral Lunar Eclipses –1999 to +3000 (2000 BCE to 3000 CE) |
||||
| Quincena Solar Eclipse |
QSE | Number | Percent | Recent Examples (Years) |
| – total | –t | 878 | 20.1% | …, 2002, 2006, 2009, 2020, 2024,… |
| total – | t– | 848 | 19.4% | …, 1998, 2009, 2012, 2016, 2027,… |
| – annular | –a | 1144 | 26.1% | …, 1999, 2002, 2017, 2020, 2031,… |
| annular – | a– | 1128 | 25.8% | …, 2001, 2002, 2009, 2013, 2016,… |
| – hybrid | –h | 176 | 4.0% | …, 1846, 1908, 2013, 2031, 2049,… |
| hybrid – | h– | 204 | 4.7% | …, 1987, 2005, 2023, 2172, 2190,… |
Acknowledgments
The information presented on this web page is based on material originally published in Five Millennium Canon of Lunar Eclipses: -1999 to +3000 and Five Millennium Catalog of Lunar Eclipses: -1999 to +3000. All eclipse calculations are by Fred Espenak, and he assumes full responsibility for their accuracy.
Permission is freely granted to reproduce this data when accompanied by an acknowledgment:
"Eclipse Predictions by Fred Espenak and Jean Meeus, www.EclipseWise.com"
The use of diagrams and maps is permitted provided that they are NOT altered (except for re-sizing) and the embedded credit line is NOT removed or covered.
References
Espenak, F., and Meeus, J., Five Millennium Canon of Lunar Eclipses: -1999 to +3000, Astropixels Publishing, Portal, AZ (2022).
Espenak, F., and Meeus, J., Five Millennium Catalog of Lunar Eclipses: -1999 to +3000, Astropixels Publishing, Portal, AZ (2022).
Gingerich, O., (Translator), Canon of Eclipses, Dover Publications, New York (1962) (from the original T.R. von Oppolzer, book, Canon der Finsternisse, Wien, [1887]).
Meeus, J., Mathematical Astronomy Morsels, Willmann-Bell, Richmond, Virginia, pp. 108–110, (1997).
Meeus, J., More Mathematical Astronomy Morsels, Willmann-Bell, Richmond, Virginia, pp. 120–126 (2002).
Meeus, J., Mathematical Astronomy Morsels III, Willmann-Bell, Richmond, Virginia, pp. 109–111, (2004a).
Meeus, J., Grosjean, C.C., and Vanderleen, W., Canon of Solar Eclipses, Pergamon Press, Oxford, United Kingdom (1966).
van den Bergh, G., Periodicity and Variation of Solar (and Lunar) Eclipses, Tjeenk Willink, and Haarlem, Netherlands (1955).
von Oppolzer, T.R., Canon der Finsternisse, Wien, (1887).
Relevant Links:
Six Millennium Catalog of Lunar Eclipses
Lunar Eclipse Statistics
Periodicity of Lunar Eclipses
Catalog of Lunar Eclipse Saros Series
![]()
Eclipses and the Moon's Orbit
Eclipses and the Saros
![]()
Six Millennium Catalog of Solar Eclipses
Solar Eclipse Statistics
Periodicity of Solar Eclipses
Catalog of Solar Eclipse Saros Series
Links to Additional Lunar Eclipse Predictions
- Home - home page of EclipseWise with predictions for both solar and lunar eclipses
- Lunar Eclipses - primary page for lunar eclipse predictions
- Lunar Eclipse Links - detailed directory of links
- Six Millennium Catalog of Lunar Eclipses - covers the years -2999 to +3000 (3000 BCE to 3000 CE)
- Javascript Lunar Eclipse Explorer - calculate all lunar eclipses visible from a city
- Five Millennium Canon of Lunar Eclipses: -1999 to +3000 - link to the publication
- Five Millennium Catalog of Lunar Eclipses: -1999 to +3000 - link to the publication
- Thousand Year Canon of Lunar Eclipses 1501 to 2500 - link to the publication
- MrEclipse.com - eclipse resources and tips on photography
- Lunar Eclipses for Beginners - a primer on lunar eclipse basics
- How to Photograph a Lunar Eclipse - instructions for imaging an eclipse of the Sun
- MrEclipse Photo Index - an index of lunar eclipse photographs




