Solar Eclipse Prime Page
Annular Solar Eclipse of 2046 Feb 05
Fred Espenak
Key to Solar Eclipse Figure (below)
Introduction
The Annular Solar Eclipse of 2046 Feb 05 is visible from the following geographic regions:
- Partial Eclipse: Australia, Papua New Guinea, west U.S.
- Annular Eclipse: Papua New Guinea, Hawaii, California, Oregon, Idaho
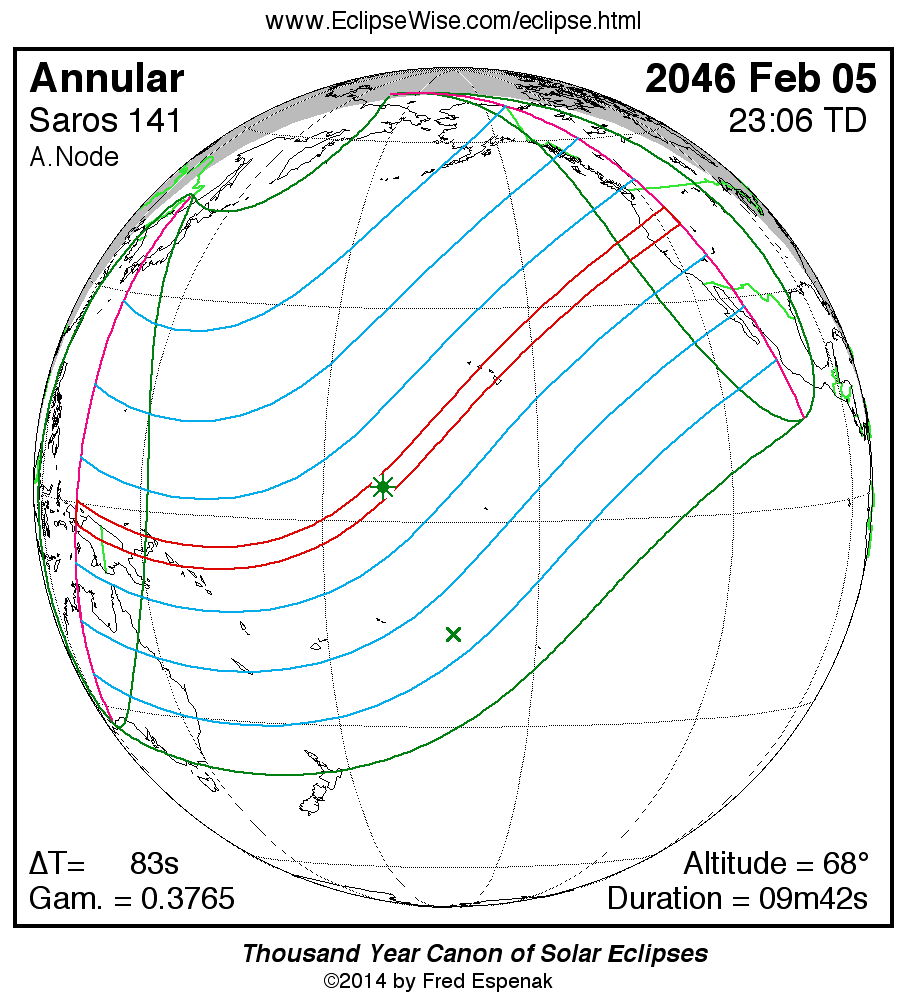
The map to the right depicts the geographic regions of eclipse visibility. Click on the map to enlarge it. For an explanation of the features appearing in the map, see Key to Solar Eclipse Maps.
The instant of greatest eclipse takes place on 2046 Feb 05 at 23:06:26 TD (23:05:04 UT1). This is 2.3 days before the Moon reaches apogee. During the eclipse, the Sun is in the constellation Capricornus. The synodic month in which the eclipse takes place has a Brown Lunation Number of 1523.
The eclipse belongs to Saros 141 and is number 25 of 70 eclipses in the series. All eclipses in this series occur at the Moon’s ascending node. The Moon moves southward with respect to the node with each succeeding eclipse in the series and gamma decreases.
The solar eclipse of 2046 Feb 05 is an exceptionally long annular eclipse with a duration at greatest eclipse of 09m42s. It has an eclipse magnitude of 0.9232.
The annular solar eclipse of 2046 Feb 05 is preceded two weeks earlier by a partial lunar eclipse on 2046 Jan 22.
These eclipses all take place during a single eclipse season.
The eclipse predictions are given in both Terrestrial Dynamical Time (TD) and Universal Time (UT1). The parameter ΔT is used to convert between these two times (i.e., UT1 = TD - ΔT). ΔT has a value of 81.8 seconds for this eclipse.
The following links provide maps and data for the eclipse.
- Orthographic Map: Annular Solar Eclipse of 2046 Feb 05 - detailed global map of eclipse visibility (Key to Figure)
- Google Map: Annular Solar Eclipse of 2046 Feb 05 - interactive map of the eclipse path
- Path Table: Annular Solar Eclipse of 2046 Feb 05 - coordinates of the central line and path limits
- Circumstances Table: Annular Solar Eclipse of 2046 Feb 05 - eclipse times for hundreds of cities
- Saros 141 Table - data for all eclipses in the Saros series
- Additional Tables and Data - for this event
Global Map Animation of Solar Eclipse
Michael Zeiler GreatAmericanEclipse.com and
Fred Espenak EclipseWise.com
have created a series of eclipse animations - one for every solar eclipse during the 21st Century.
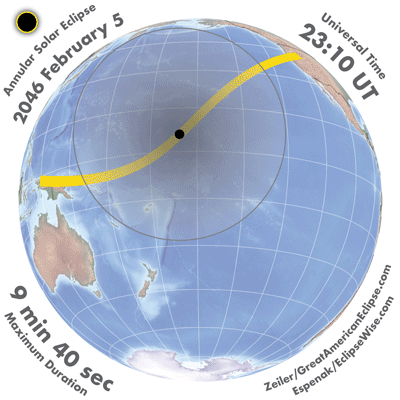
The animation of the Annular Solar Eclipse of 2046 Feb 05 shows the path of the Moon's shadows as they sweep across a global map of Earth (an orthographic projection). The vantage point of the animation is as seen from the Moon. The daylight hemisphere of Earth then faces the Moon and the lunar shadows appear perfectly circular with no distorted projection effects as they race across Earth.
The Moon's antumbral shadow appears as a small black disk and tracks along the path of annularity (yellow strip). The much larger penumbral shadow is lightly shaded and is outlined with a solid black edge. A partial eclipse is visible from within the penumbra, while an annular eclipse is visible inside the antumbra. Another consequence of this viewing geometry is that the Moon's shadows move across the disk of Earth in a straight line.
The map to the right shows a single frame from the medium size animation for the Annular Solar Eclipse of 2046 Feb 05 . In the upper left corner is the type of eclipse and the eclipse date. To the upper right is the Universal Time. The lower left corner displays the instantaneous duration of annularity. To the lower right is the credit for the animation.
Animations for the Annular Solar Eclipse of 2046 Feb 05 are available in three sizes/resolutions: small, medium, and large. They can be viewed through the following links:
- Small Animation (size 300 x 300 pixels)
- Medium Animation (size 400 x 400 pixels)
- Large Animation (size 800 x 800 pixels)

These animations may be freely used and shared through Creative Commons.
You may use and distribute these eclipse animations as long as they are not modified and you include an attribution.
Solar Eclipse Global Animation by
Fred Espenak and Michael Zeiler
is licensed under a Creative Commons Attribution-NoDerivatives 4.0 International License.
Based on work at EclipseWise.com
and GreatAmericanEclipse.com
Attribution: "Global Map Animation of Eclipse courtesy of Michael Zeiler (GreatAmericanEclipse.com) and Fred Espenak (EclipseWise.com)".
- Global Map Animations of Solar Eclipsess: 2001 - 2100 - animations of every solar eclipse during the 21st Century
Eclipse Data: Annular Solar Eclipse of 2046 Feb 05
| Eclipse Characteristics | |
| Parameter | Value |
| Eclipse Magnitude | 0.92321 |
| Eclipse Obscuration | 0.85231 |
| Gamma | 0.37654 |
| Conjunction Times | ||
| Event | Calendar Date and Time | Julian Date |
| Greatest Eclipse | 2046 Feb 05 at 23:06:26.2 TD (23:05:04.3 UT1) | 2468382.461856 |
| Ecliptic Conjunction | 2046 Feb 05 at 23:10:57.3 TD (23:09:35.4 UT1) | 2468382.464993 |
| Equatorial Conjunction | 2046 Feb 05 at 23:25:48.6 TD (23:24:26.7 UT1) | 2468382.475309 |
| Geocentric Coordinates of Sun and Moon | ||
| 2046 Feb 05 at 23:06:26.2 TD (23:05:04.3 UT1) | ||
| Coordinate | Sun | Moon |
| Right Ascension | 21h19m00.8s | 21h18m27.2s |
| Declination | -15°38'42.4" | -15°20'02.1" |
| Semi-Diameter | 16'13.2" | 14'46.0" |
| Eq. Hor. Parallax | 08.9" | 0°54'11.7" |
| Geocentric Libration of Moon | |
| Angle | Value |
| l | 1.9° |
| b | -0.4° |
| c | -16.1° |
| Prediction Parameters | |
| Paramater | Value |
| Ephemerides | JPL DE405 |
| ΔT | 81.8 s |
| k (penumbra) | 0.2725076 |
| k (umbra) | 0.2722810 |
| Saros Series | 141 (25/70) |
Penumbral Shadow Contacts and Extremes: Annular Solar Eclipse of 2046 Feb 05
| Contacts of Penumbral Shadow with Earth | |||||
| Contact Event | Contact | Time TD |
Time UT1 |
Latitude | Longitude |
| First External Contact | P1 | 20:05:17.8 | 20:03:56.0 | 09°16.2'S | 149°52.9'E |
| First Internal Contact | P2 | 22:42:57.6 | 22:41:35.8 | 37°17.7'N | 125°24.7'E |
| Last Internal Contact | P3 | 23:29:25.4 | 23:28:03.6 | 73°55.4'N | 154°49.4'W |
| Last External Contact | P4 | 02:07:29.5 | 02:06:07.7 | 35°54.1'N | 129°42.7'W |
| Extreme Northern and Southern Path Limits of Penumbra | |||||
| Contact Event | Contact | Time TD |
Time UT1 |
Latitude | Longitude |
| North Extreme Path Limit 1 | N1 | 22:26:15.3 | 22:24:53.4 | 46°19.2'N | 134°19.9'E |
| South Extreme Path Limit 1 | S1 | 21:19:03.8 | 21:17:42.0 | 33°12.6'S | 123°29.1'E |
| North Extreme Path Limit 2 | N2 | 23:45:52.4 | 23:44:30.6 | 73°24.1'N | 167°15.5'E |
| South Extreme Path Limit 2 | S2 | 00:53:57.7 | 00:52:35.8 | 12°00.1'N | 103°04.1'W |
Explanation of Penumbral Shadow Contacts and Extremes Tables
Umbral Shadow Contacts and Extremes: Annular Solar Eclipse of 2046 Feb 05
| Contacts of Umbral Shadow with Earth | |||||
| Contact Event | Contact | Time TD |
Time UT1 |
Latitude | Longitude |
| First External Contact | U1 | 21:13:07.7 | 21:11:45.8 | 01°51.8'S | 135°01.6'E |
| First Internal Contact | U2 | 21:20:02.1 | 21:18:40.3 | 00°38.8'S | 133°38.5'E |
| Last Internal Contact | U3 | 00:52:36.8 | 00:51:14.9 | 44°16.3'N | 115°08.7'W |
| Last External Contact | U4 | 00:59:34.4 | 00:58:12.5 | 43°05.6'N | 116°13.8'W |
| Extreme Northern and Southern Path Limits of Umbra | |||||
| Contact Event | Contact | Time TD |
Time UT1 |
Latitude | Longitude |
| North Extreme Path Limit 1 | N1 | 21:17:28.6 | 21:16:06.8 | 00°20.3'N | 134°33.4'E |
| South Extreme Path Limit 1 | S1 | 21:15:46.1 | 21:14:24.3 | 02°51.9'S | 134°05.1'E |
| North Extreme Path Limit 2 | N2 | 00:55:10.3 | 00:53:48.5 | 45°13.2'N | 116°19.9'W |
| South Extreme Path Limit 2 | S2 | 00:56:55.5 | 00:55:33.7 | 42°07.4'N | 115°03.0'W |
Central Line Extremes and Duration: Annular Solar Eclipse of 2046 Feb 05
| Extreme Limits of the Central Line | |||||
| Contact Event | Contact | Time TD |
Time UT1 |
Latitude | Longitude |
| Extreme Central Line Limit 1 | C1 | 21:16:34.4 | 21:15:12.6 | 01°16.4'S | 134°19.8'E |
| Extreme Central Line Limit 2 | C2 | 00:56:06.1 | 00:54:44.2 | 43°40.0'N | 115°40.6'W |
Explanation of Central Line Extremes Table
| Greatest Eclipse and Greatest Duration | ||||||||
| Event | Time TD |
Time UT1 |
Latitude | Longitude | Sun Altitude |
Sun Azimuth |
Path Width | Central Duration |
| Greatest Eclipse | 23:06:26.2 | 23:05:04.3 | 04°46.9'N | 171°25.6'W | 67.9° | 157.4° | 310.1 km | 09m42.38s |
| Greatest Duration | 22:50:22.5 | 22:49:00.6 | 01°56.1'N | 174°40.8'W | 66.4° | 138.7° | 316.7 km | 09m45.63s |
Polynomial Besselian Elements: Annular Solar Eclipse of 2046 Feb 05
| Polynomial Besselian Elements | ||||||
| 2046 Feb 05 at 23:00:00.0 TD (=t0) | ||||||
| n | x | y | d | l1 | l2 | μ |
| 0 | -0.19963 | 0.32384 | -15.6473 | 0.57338 | 0.02709 | 161.5114 |
| 1 | 0.46411 | 0.20130 | 0.0123 | 0.00005 | 0.00005 | 15.0005 |
| 2 | -0.00004 | 0.00007 | 0.0000 | -0.00001 | -0.00001 | 0.0000 |
| 3 | -0.00001 | -0.00000 | - | - | - | - |
| Tan ƒ1 | 0.0047431 |
| Tan ƒ2 | 0.0047195 |
At time t1 (decimal hours), each besselian element is evaluated by:
x = x0 + x1*t + x2*t2 + x3*t3 (or x = Σ [xn*tn]; n = 0 to 3)
where: t = t1 - t0 (decimal hours) and t0 = 23.000
Links for the Annular Solar Eclipse of 2046 Feb 05
- Orthographic Map: Annular Solar Eclipse of 2046 Feb 05 - detailed global map of eclipse visibility (Key to Figure)
- Google Map: Annular Solar Eclipse of 2046 Feb 05 - interactive map of the eclipse path
- Path Table: Annular Solar Eclipse of 2046 Feb 05 - coordinates of the central line and path limits
- Circumstances Table: Annular Solar Eclipse of 2046 Feb 05 - eclipse times for hundreds of cities
- Saros 141 Table - data for all eclipses in the Saros series
- Annular Solar Eclipse of 2046 Feb 05 - Google search for links to this eclipse
Links to Additional Solar Eclipse Information
- Home - home page of EclipseWise with predictions for both solar and lunar eclipses
- Solar Eclipses - primary page for solar eclipse predictions
- Solar Eclipse Links - detailed directory of links
- Solar Eclipse Basics - the fundamentals about solar eclipses
- Periodicity of Solar Eclipses - eclipse seasons, Saros and Inex
- Solar Eclipses and the Saros - details on the Saros cycle
- Solar Eclipse Predictions and the Mean Lunar Radius
• Decade Tables of Solar Eclipses:
|
1901 - 1910 |
1911 - 1919 |
1921 - 1930 |
1931 - 1940 |
1941 - 1950 |
|
1951 - 1960 |
1961 - 1970 |
1971 - 1980 |
1981 - 1990 |
1991 - 2000 |
|
2001 - 2010 |
2011 - 2020 |
2021 - 2030 |
2031 - 2040 |
2041 - 2050 |
|
2051 - 2060 |
2061 - 2070 |
2071 - 2080 |
2081 - 2090 |
2091 - 2100 |
- Six Millennium Catalog of Solar Eclipses - covers the years -2999 to +3000 (3000 BCE to 3000 CE)
- Global Map Animations of Solar Eclipses: 2001 - 2100 - animated maps of every solar eclipse of the 21st Century
- Saros Catalog of Solar Eclipses - covers Saros series -30 through 190
- World Atlas of Solar Eclipse Maps - index page
- Solar Eclipse Search Engine - search for solar eclipses from -1999 to +3000
- Javascript Solar Eclipse Explorer - calculate all solar eclipses visible from a city
- MrEclipse.com - Eclipse resources and tips on photography
- MrEclipse: Solar Eclipses for Beginners - a primer on solar eclipse basics
- How to Photograph a Solar Eclipse - instructions for imaging an eclipse of the Sun
- MrEclipse Photo Index - an index of solar eclipse photographs
Solar Eclipse Publications
- Eclipse Almanac: 2021 to 2030 - overview of all solar and lunar eclipses for the decade
- 21st Century Canon of Solar Eclipses - coveres every solar eclipse from 2001 through 2100
- Thousand Year Canon of Solar Eclipses 1501 to 2500 - basic details about every solar eclipse for 1000 years
- Five Millennium Canon of Solar Eclipses: -1999 to +3000 - the ultimate reference with maps and diagrams
- Five Millennium Catalog of Solar Eclipses: -1999 to +3000 - the ultimate reference containing comprehensive tables
- Atlas of Central Solar Eclipses in the USA - 2,000 years of solar eclipses through North America
- Road Atlas of the Annular Solar Eclipse of 2023 October 14 - detailed maps of the annular eclipse path
- Road Atlas of the Total Solar Eclipse of 2024 April 08 - detailed maps of the total eclipse path
Eclipse Predictions
Predictions for the Annular Solar Eclipse of 2046 Feb 05 were generated using the JPL DE405 solar and lunar ephemerides. The lunar coordinates were calculated with respect to the Moon's Center of Mass. The predictions are given in both Terrestrial Dynamical Time (TD) and Universal Time (UT1). The parameter ΔT is used to convert between these two times (i.e., UT1 = TD - ΔT). ΔT has a value of 81.8 seconds for this eclipse.
Acknowledgments
Some of the content on this website is based on the books 21st Century Canon of Solar Eclipses and Thousand Year Canon of Solar Eclipses 1501 to 2500. All eclipse calculations are by Fred Espenak, and he assumes full responsibility for their accuracy.
Permission is granted to reproduce eclipse data when accompanied by a link to this page and an acknowledgment:
"Eclipse Predictions by Fred Espenak, www.EclipseWise.com"
The use of diagrams and maps is permitted provided that they are NOT altered (except for re-sizing) and the embedded credit line is NOT removed or concealed.