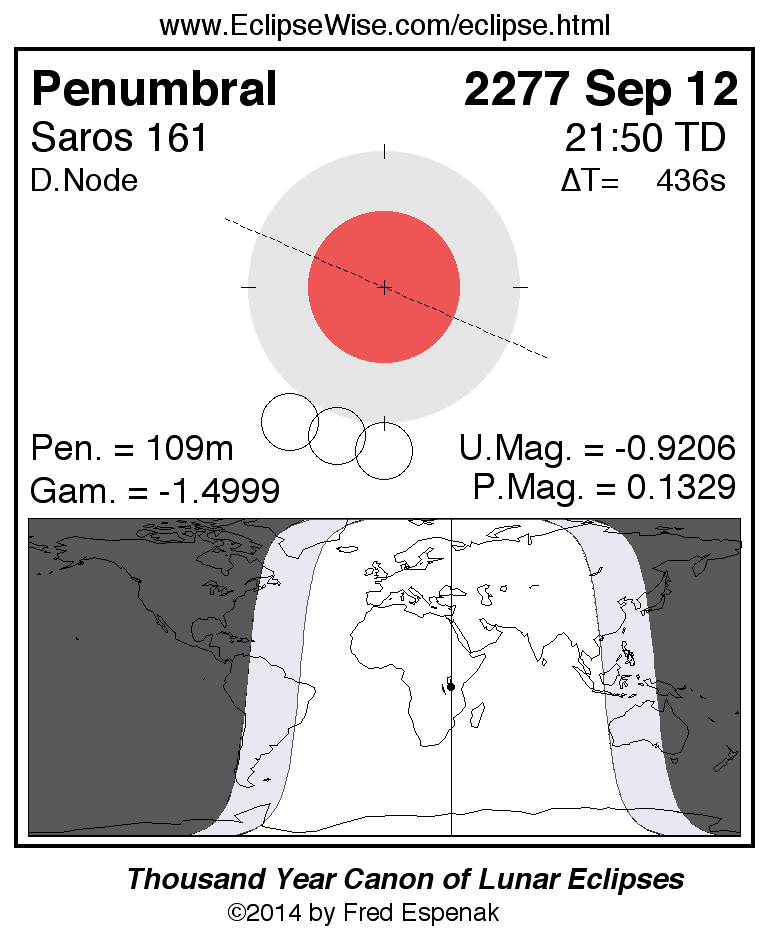
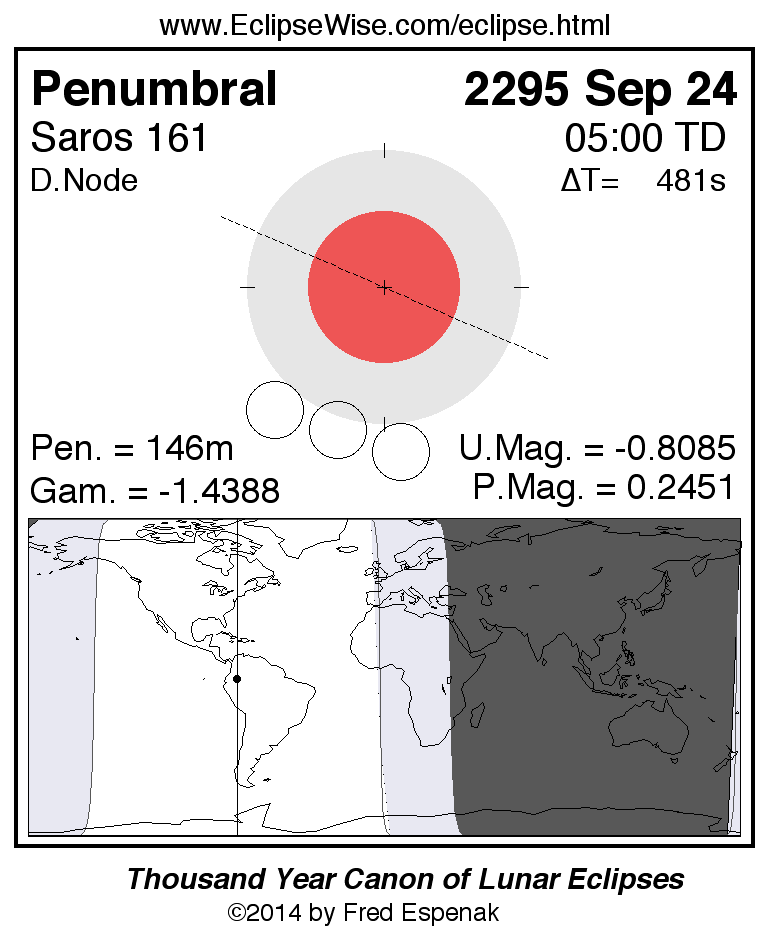
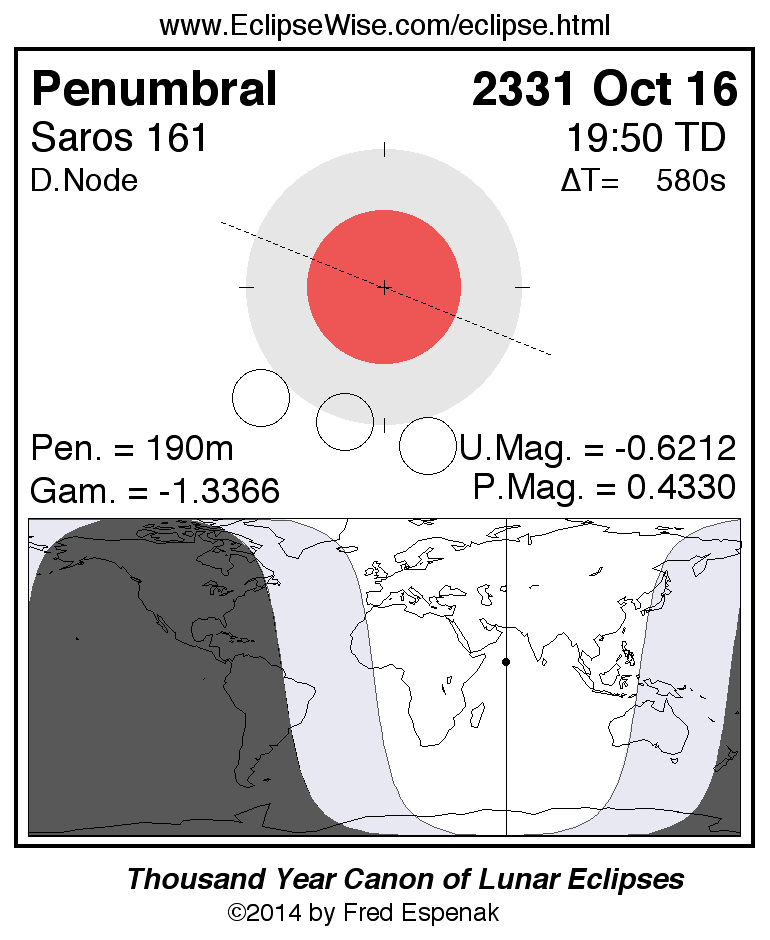
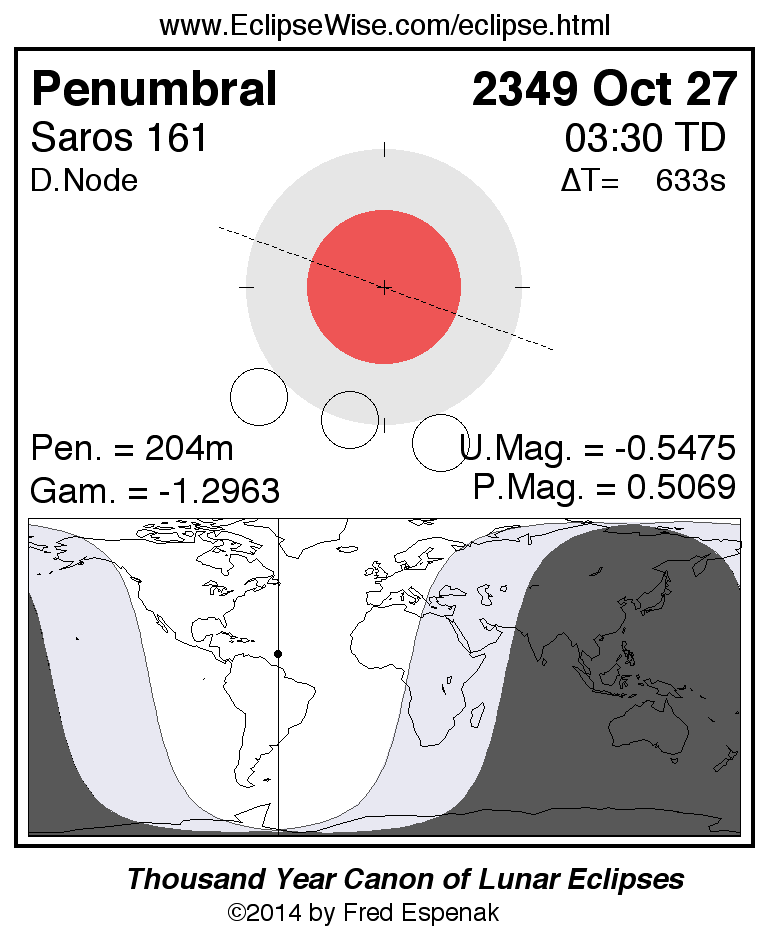
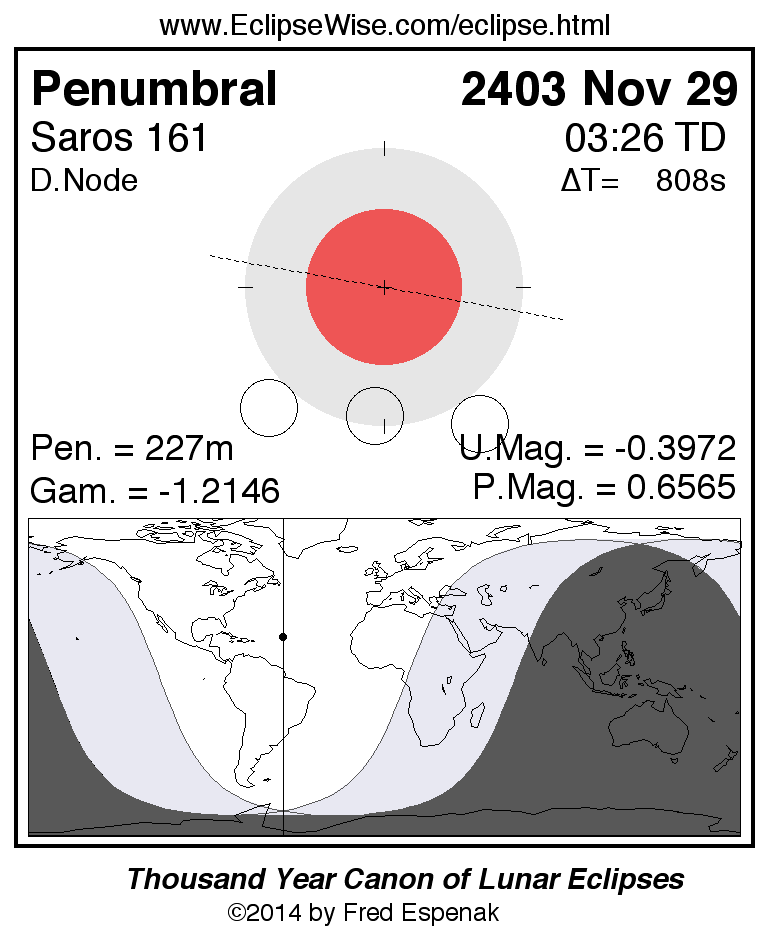
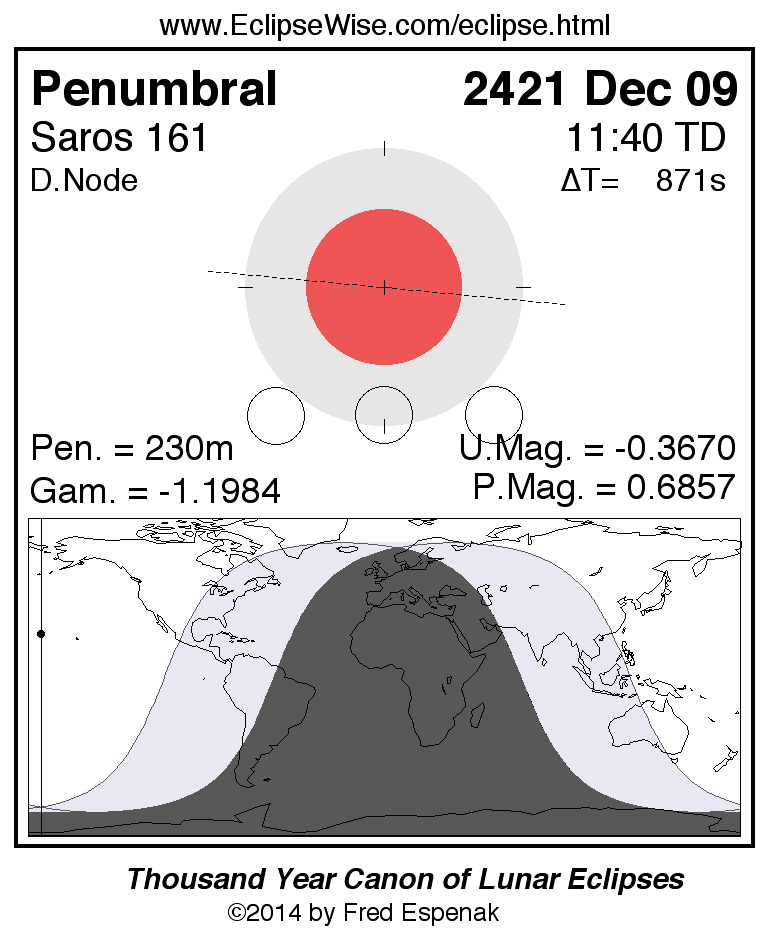
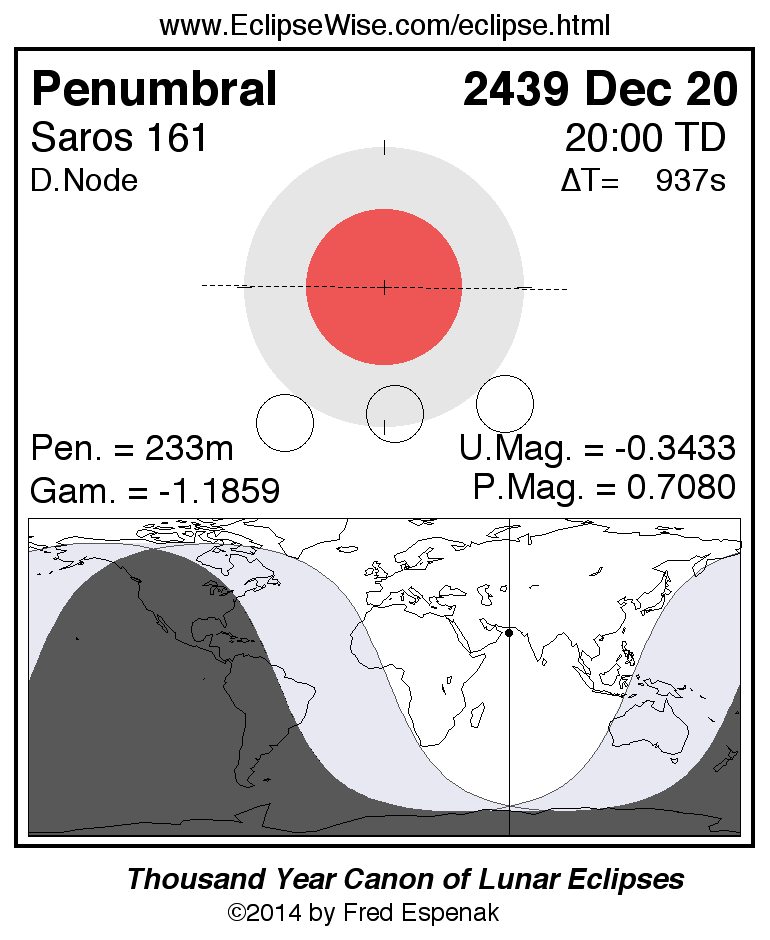
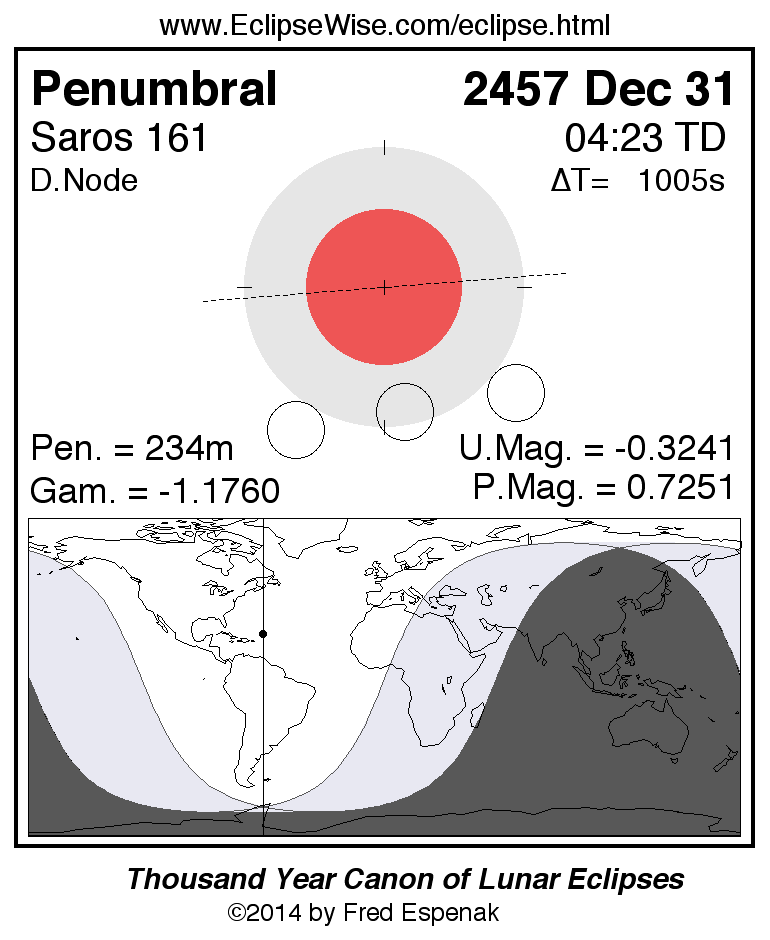
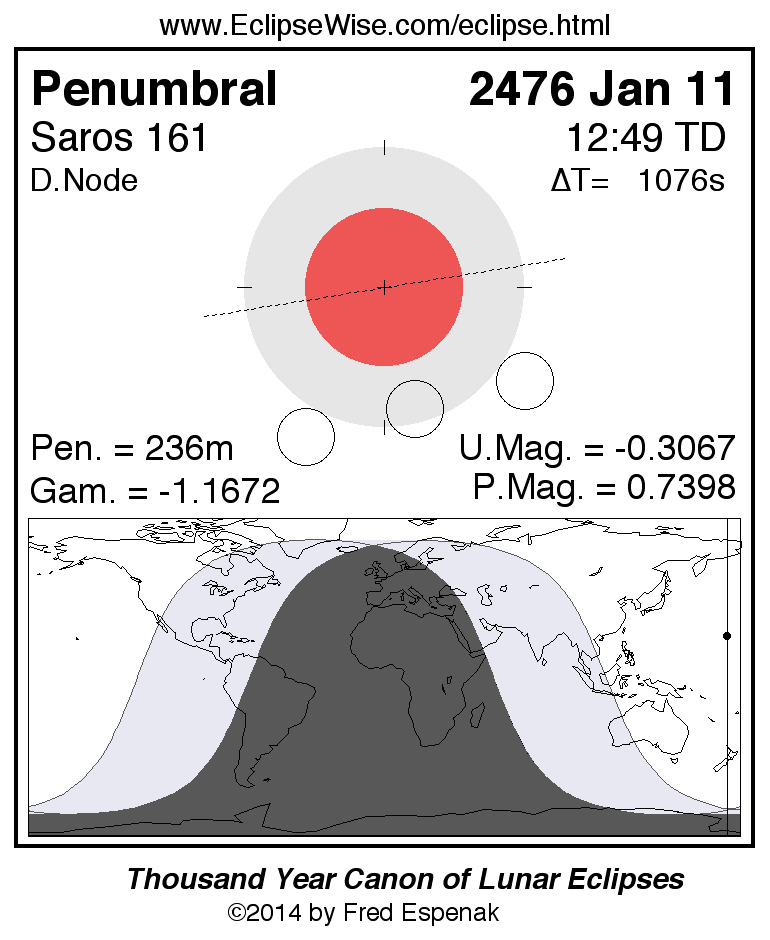
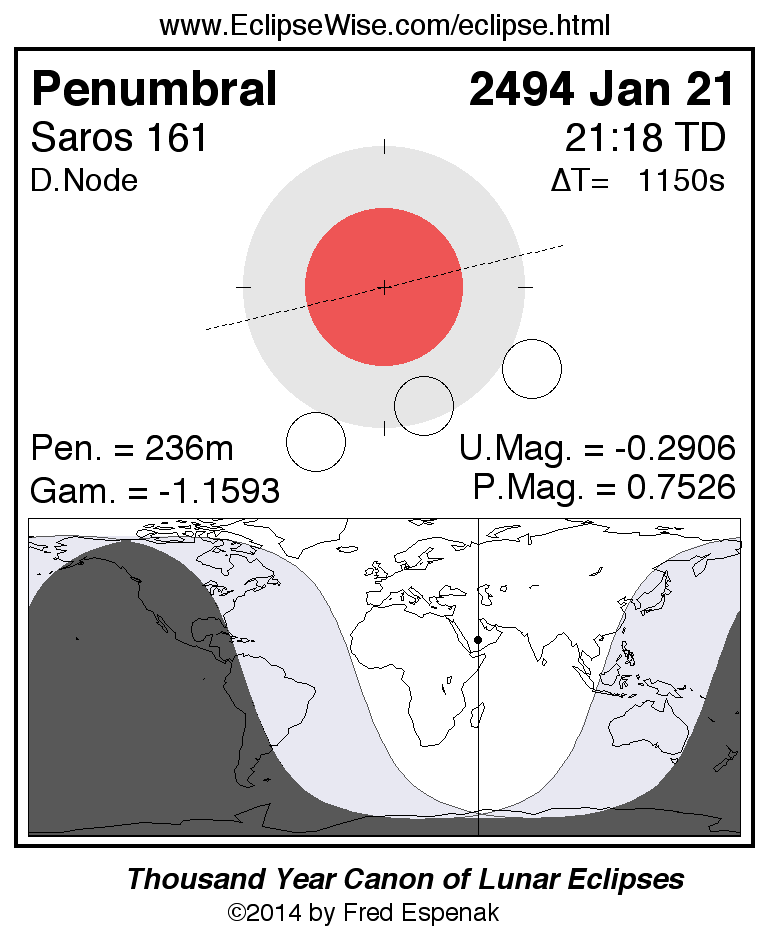
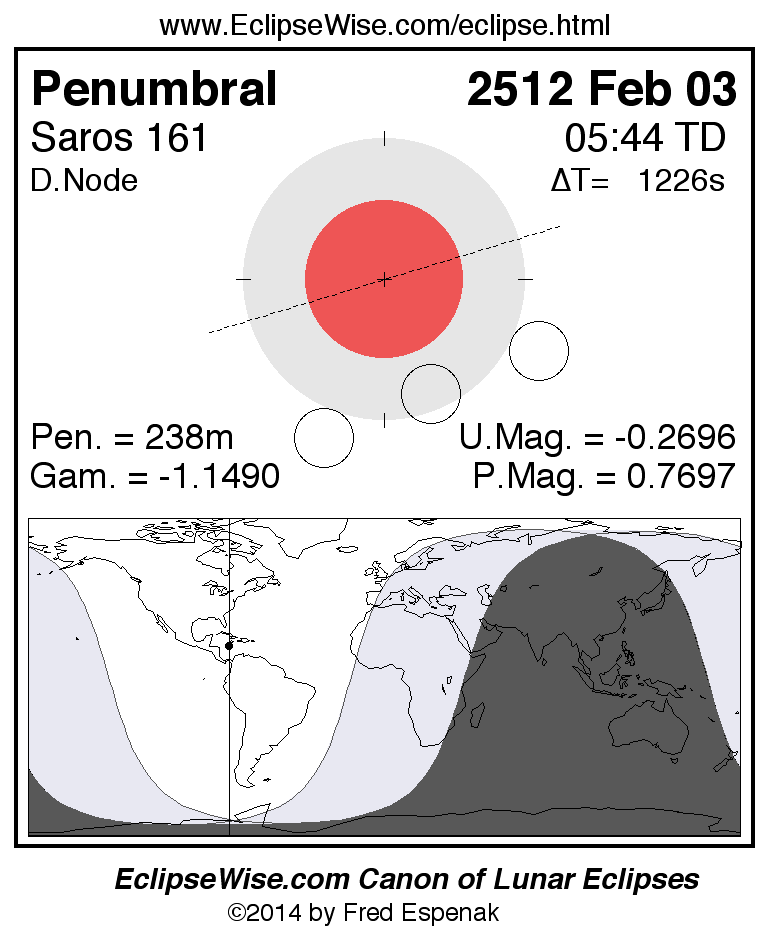
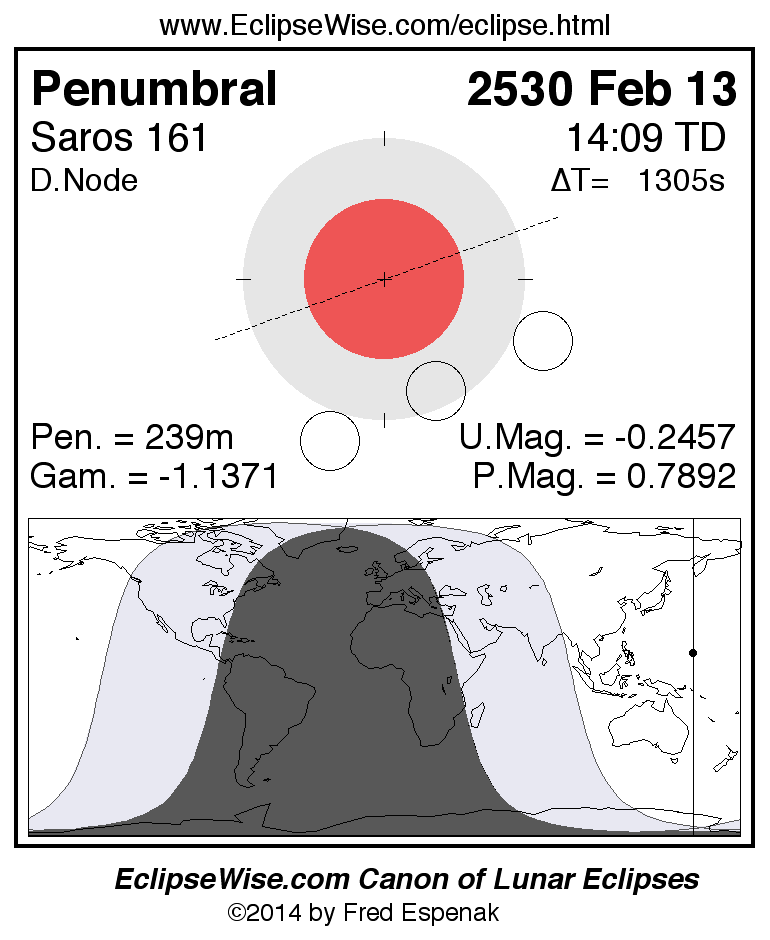
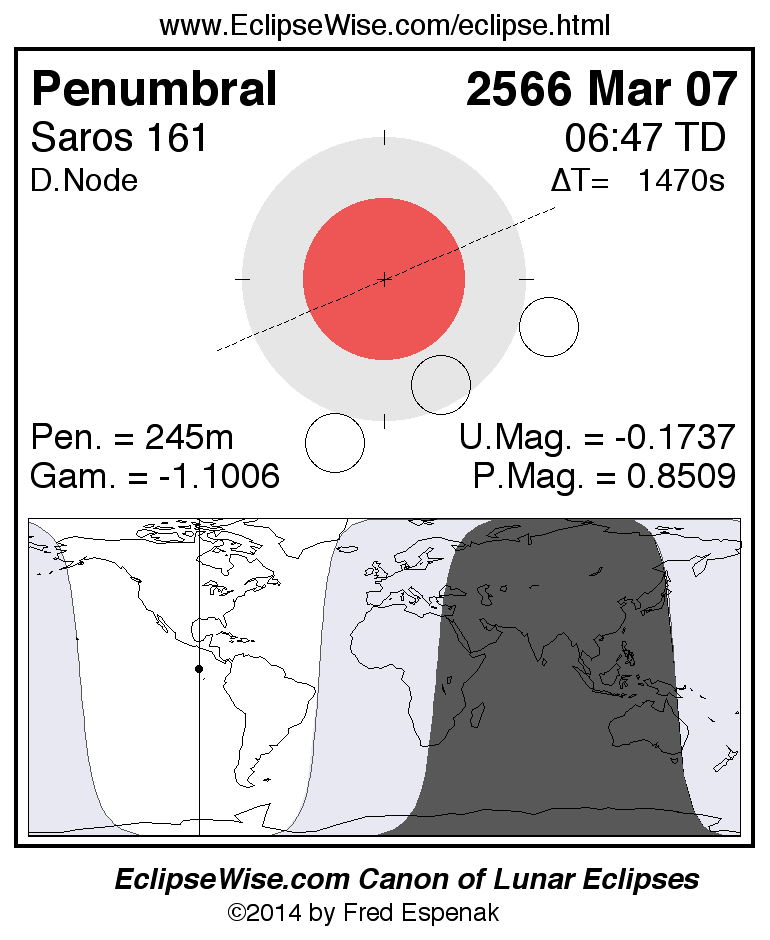
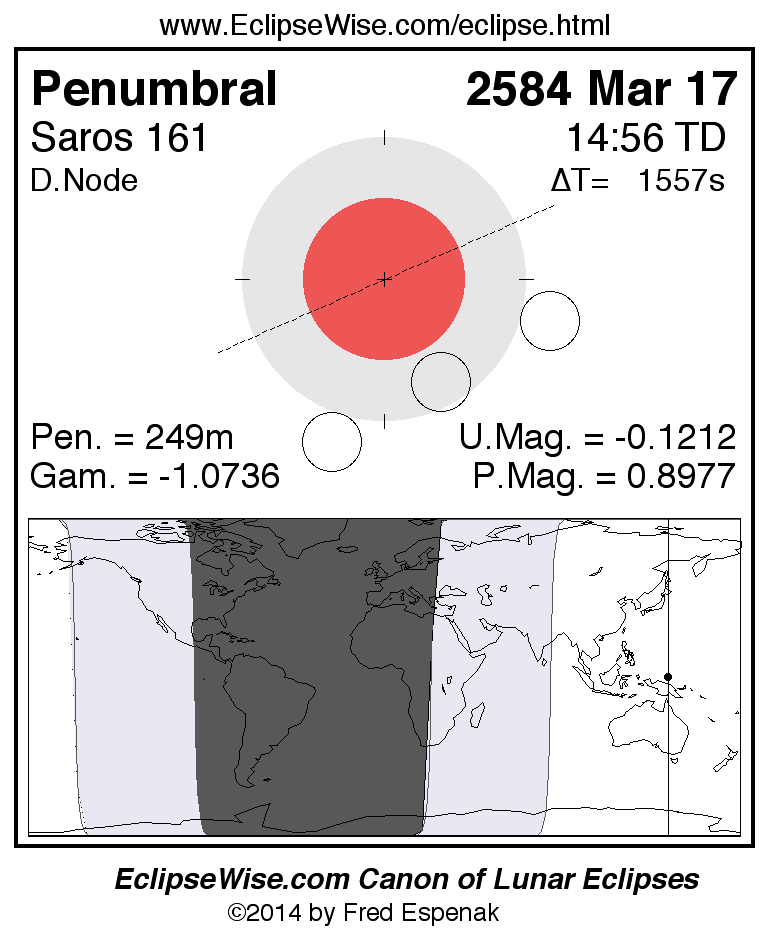
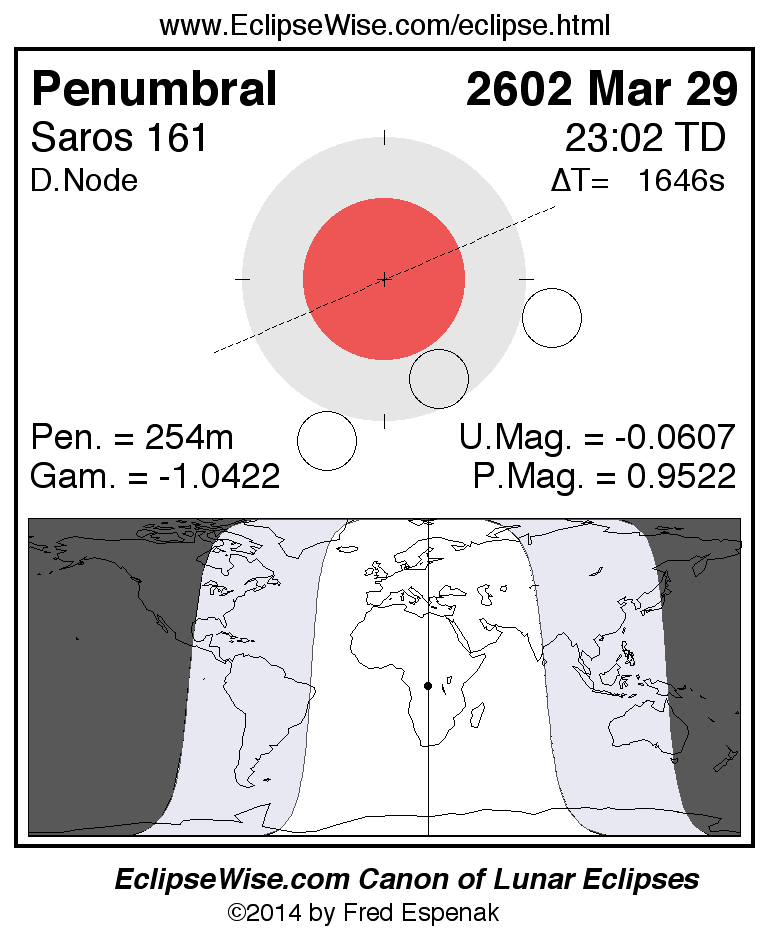
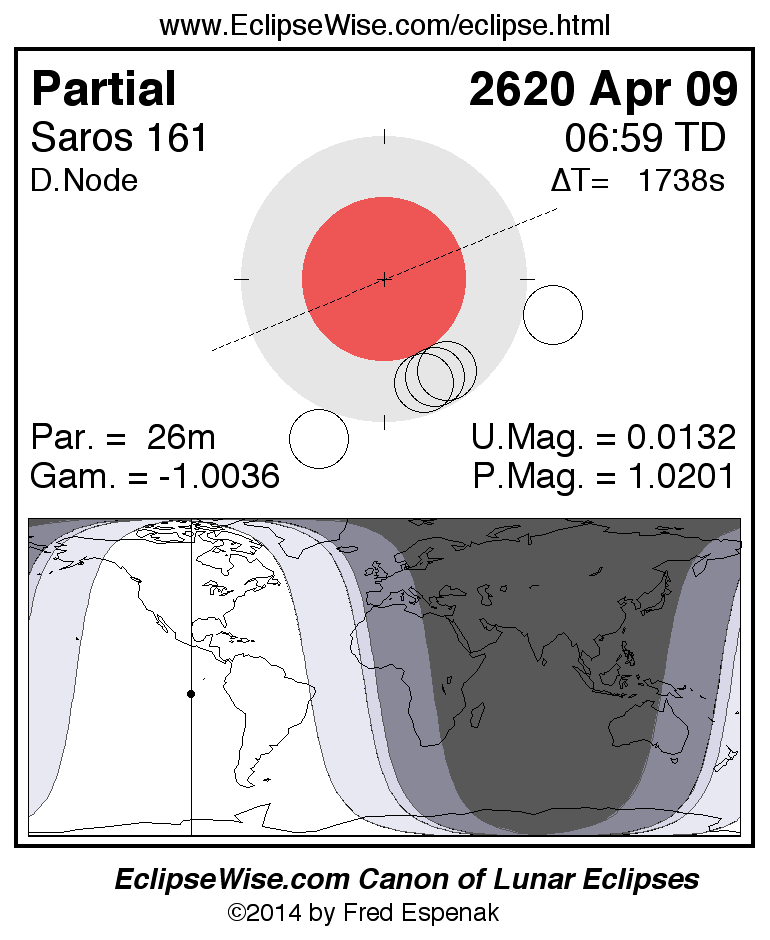
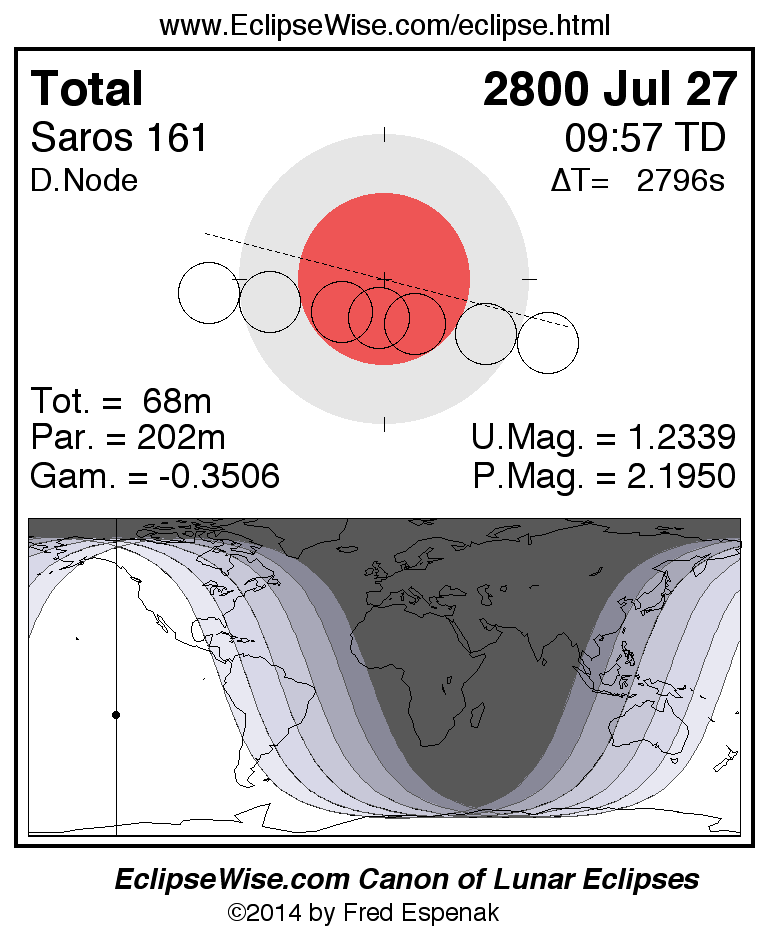
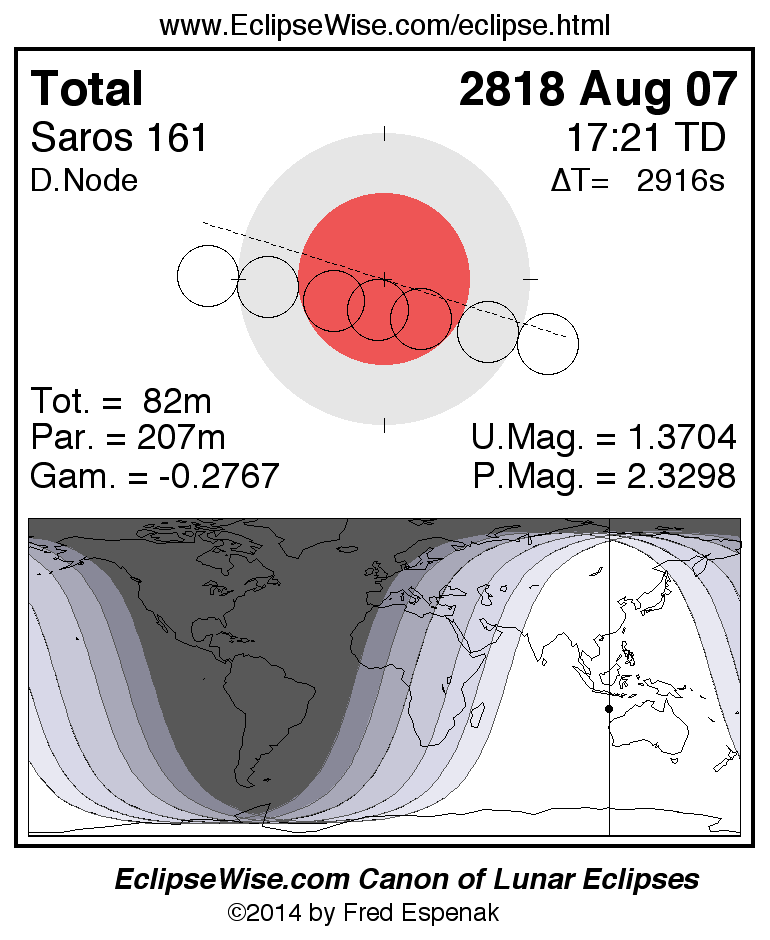
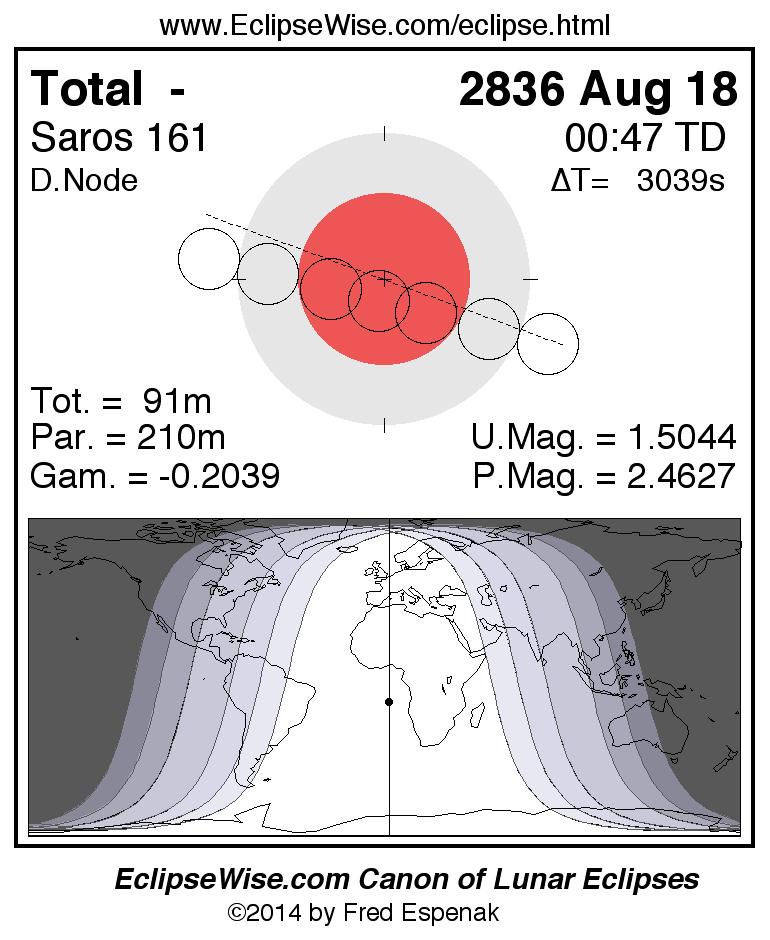
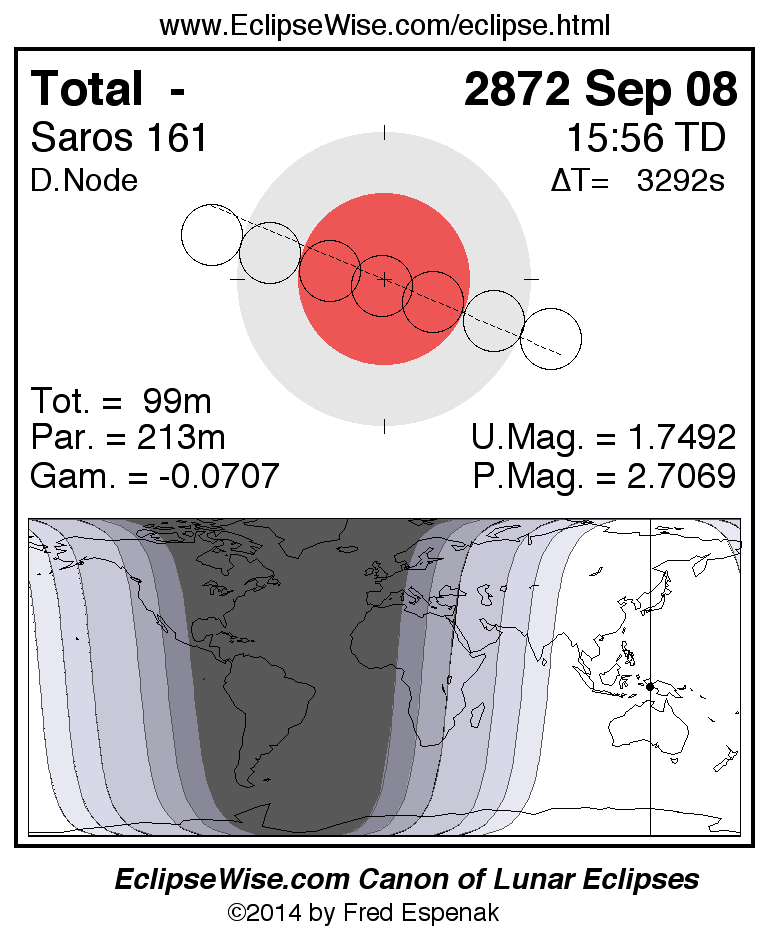
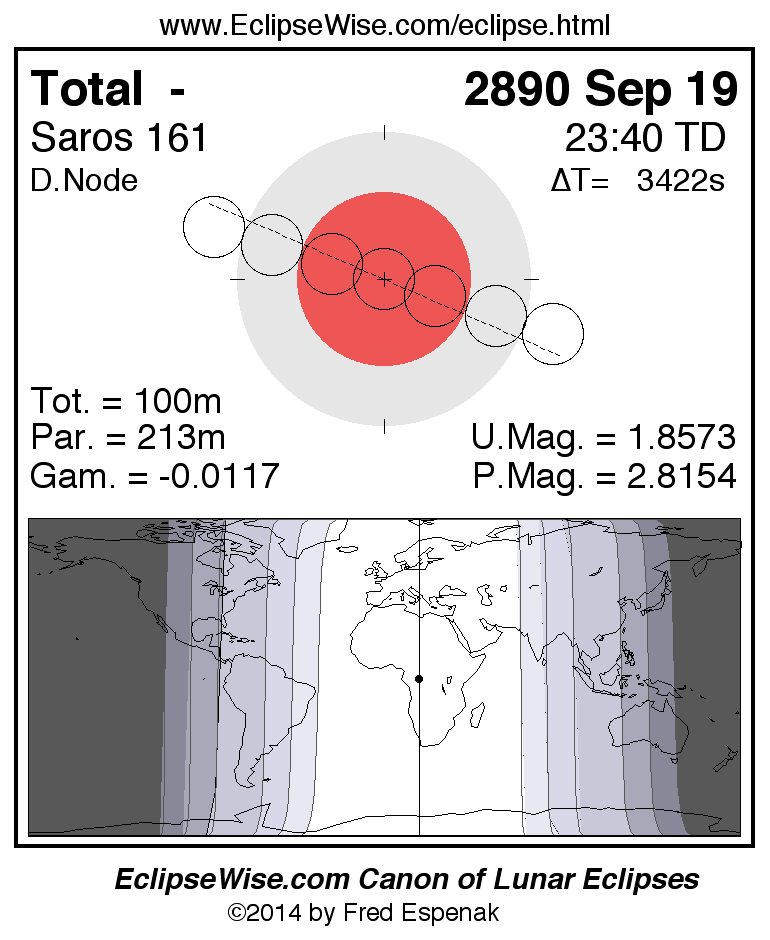
Saros 161
Panorama of Lunar Eclipses of Saros 161
Fred Espenak
Introduction
A lunar eclipse occurs whenever the Moon passes through Earth's shadow. At least two lunar eclipses and as many as five occur every year.
The periodicity and recurrence of lunar eclipses is governed by the Saros cycle, a period of approximately 6,585.3 days (18 years 11 days 8 hours). When two eclipses are separated by a period of one Saros, they share a very similar geometry. The two eclipses occur at the same node with the Moon at nearly the same distance from Earth and the same time of year due to a harmonic in three cycles of the Moon's orbit. Thus, the Saros is useful for organizing eclipses into families or series. Each series typically lasts 12 to 15 centuries and contains about 70 to 80 eclipses. Every saros series begins with a number of penumbral lunar eclipses. The series will then produce several dozen partial eclipses, followed by several dozen total eclipses. The later portion of the series produces another set of partial eclipses before ending with a final group of penumbral eclipses. The exact numbers vary from one series to the next, but the overall sequence remains the same. For more information, see Periodicity of Lunar Eclipses.
Panorama of Lunar Eclipses of Saros 161
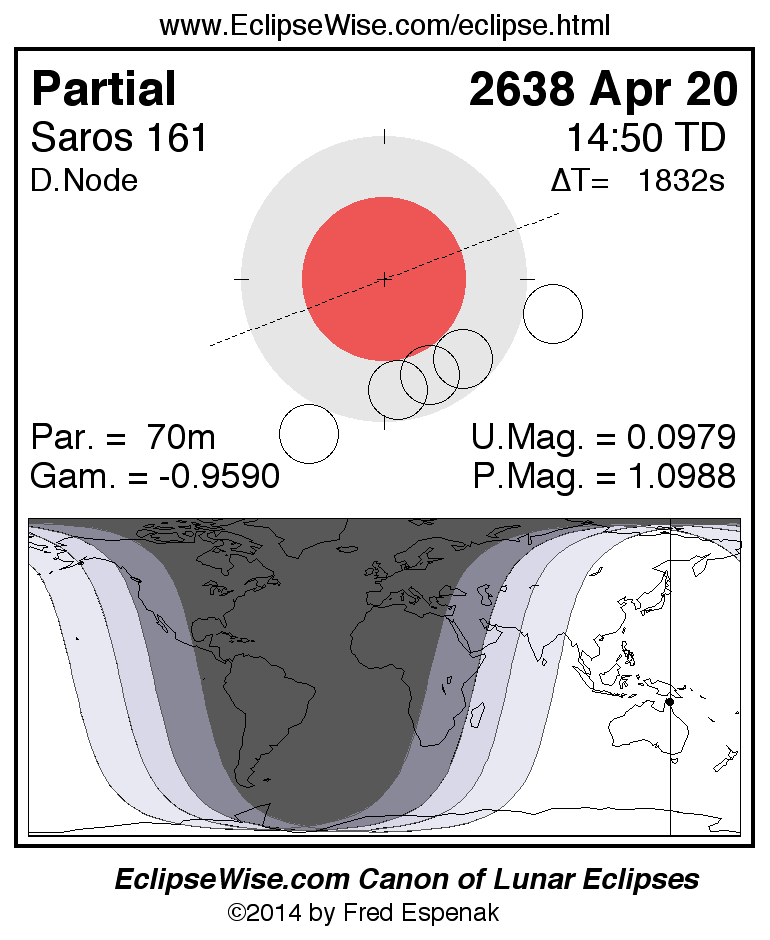
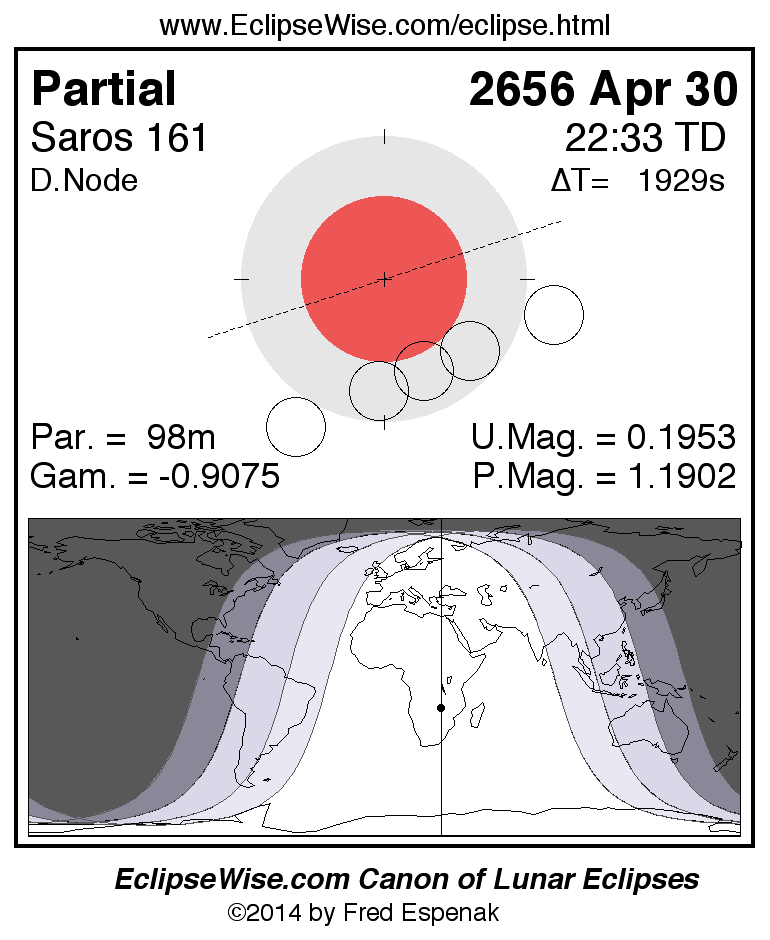
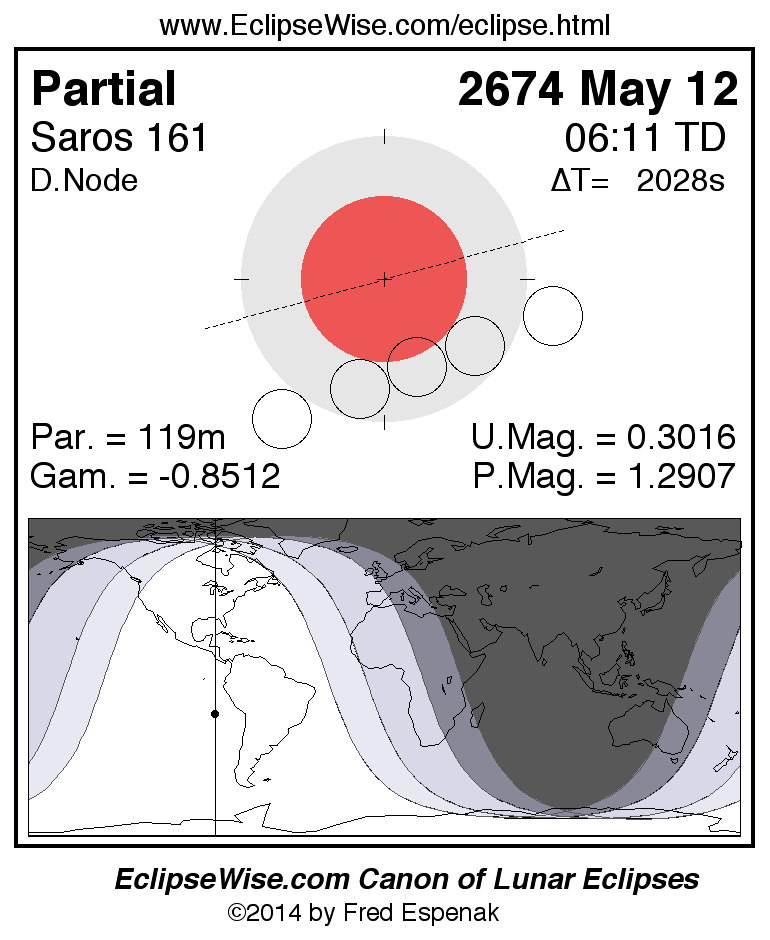
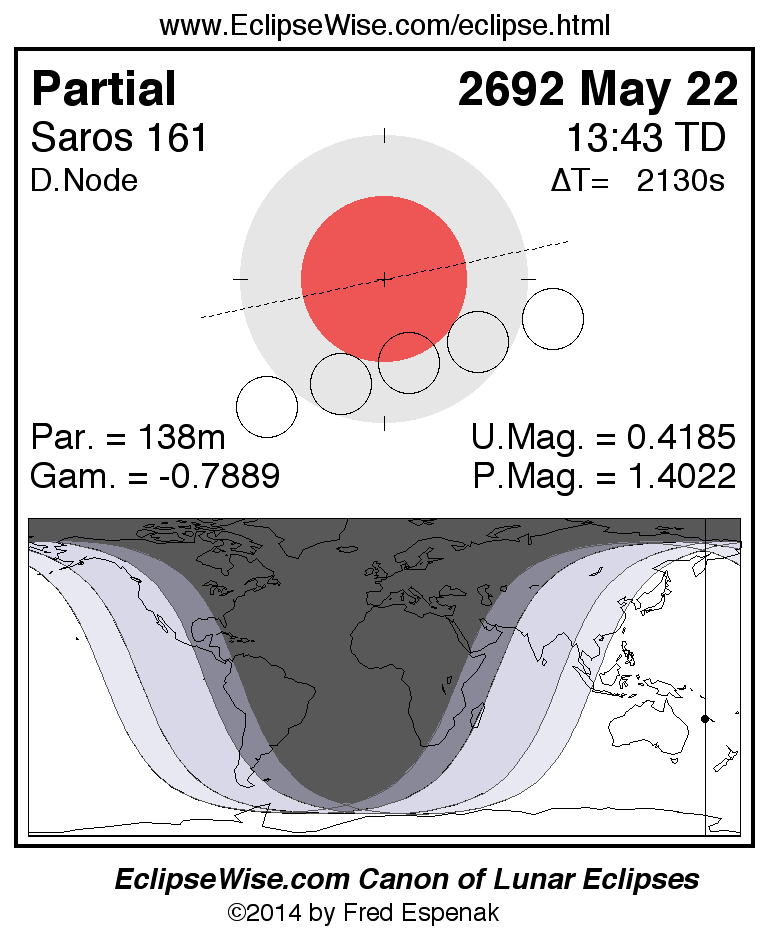
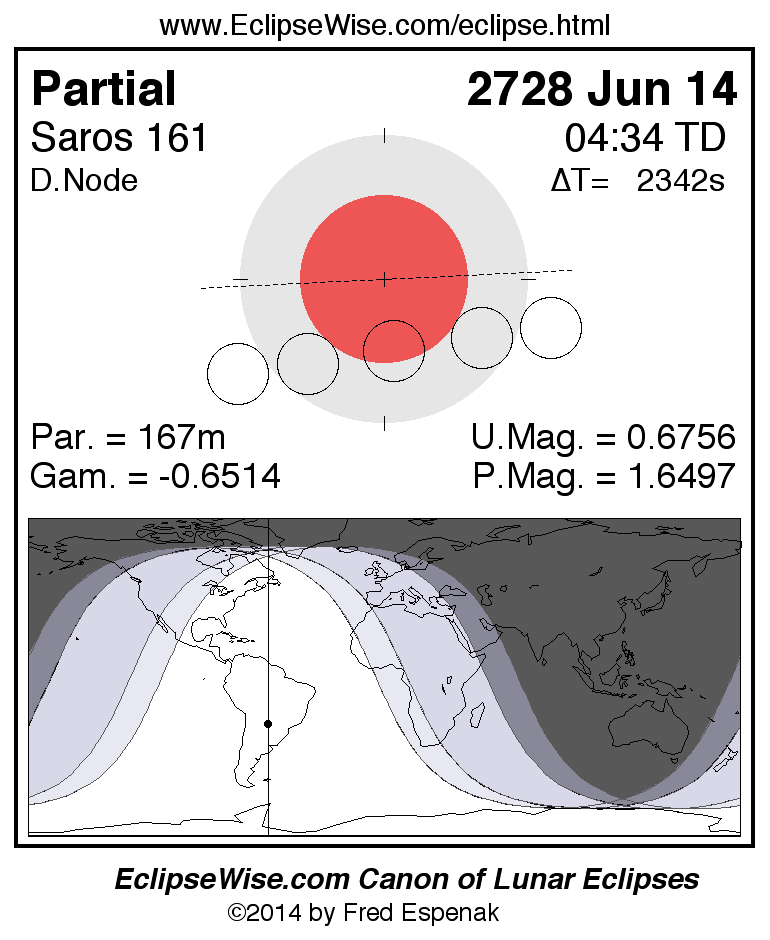
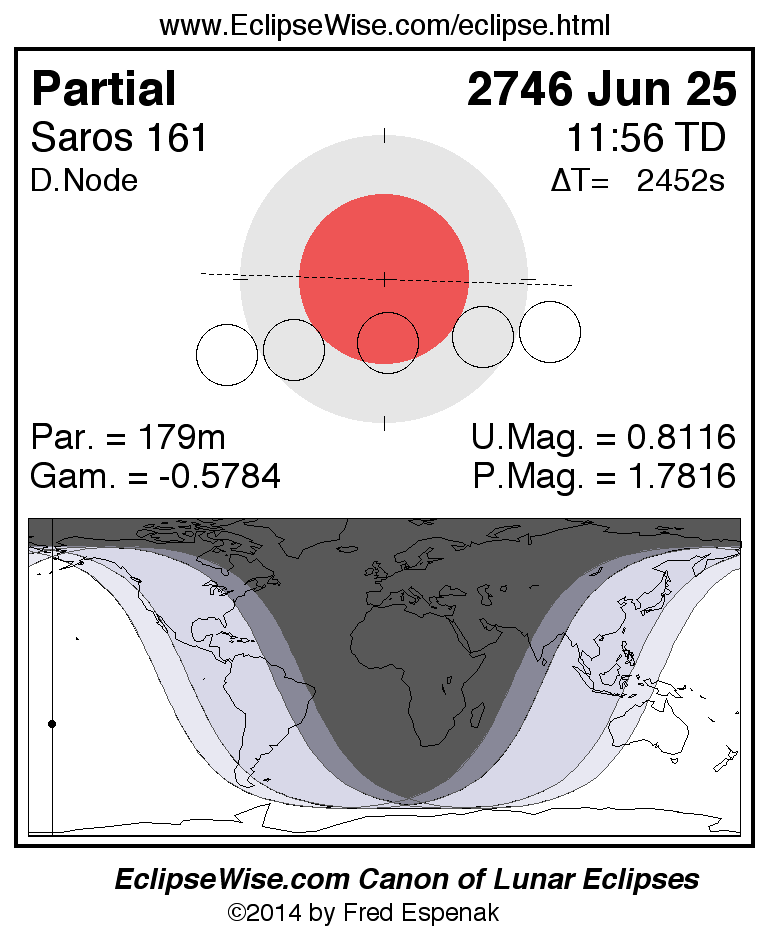
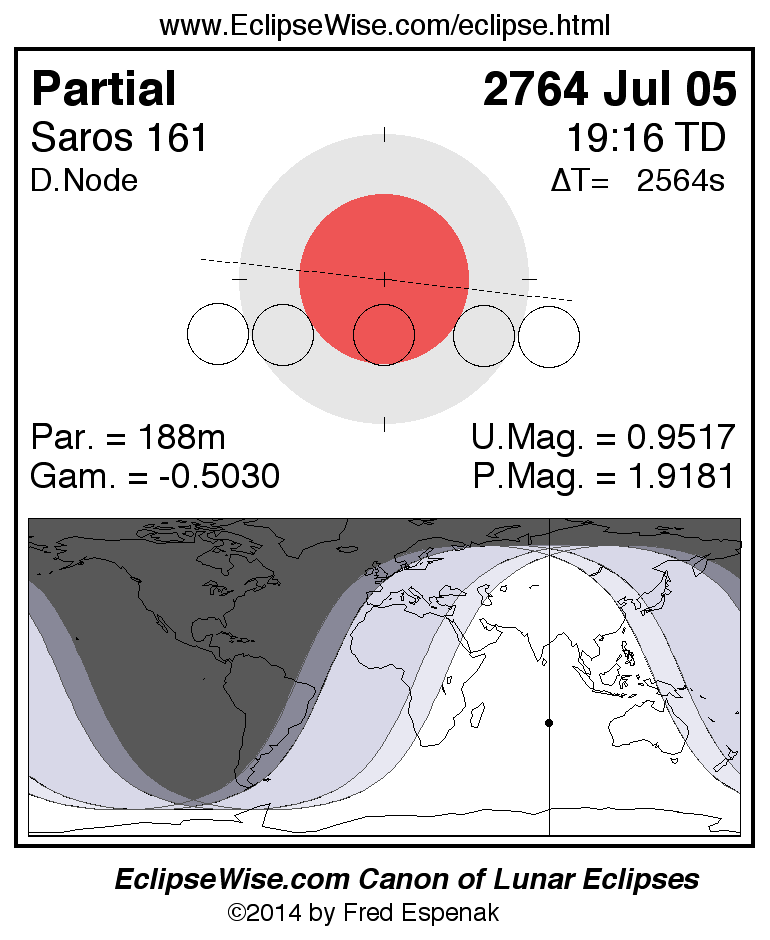
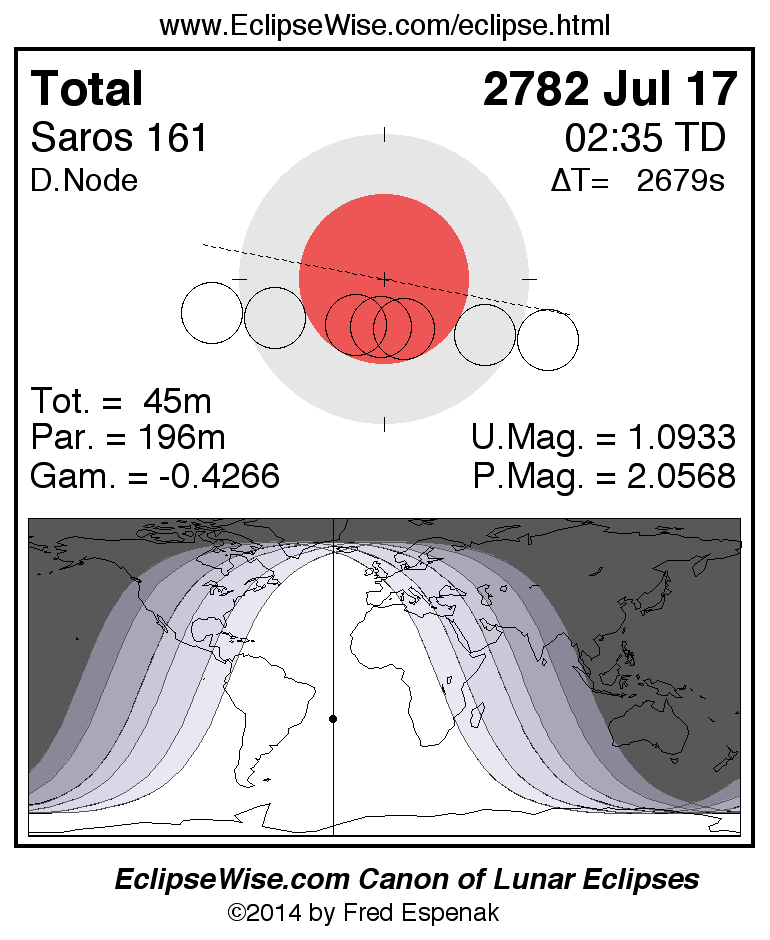
A panorama of all lunar eclipses belonging to Saros 161 is presented here. Each figure shows the Moon's path with respect to Earth's penumbral and umbral shadows. Below the path is a map depicting the geographic region of visibility for the eclipse. The date and time are given for the instant of Greatest Eclipse. Every figure serves as a hyperlink to the EclipseWise Prime page for that eclipse with a larger figure and complete details for the eclipse. Visit the Key to Lunar Eclipse Figures for a detailed explanation of these diagrams. Near the bottom of this page are a series of hyperlinks for more on lunar eclipses.
The exeligmos is a period of three Saros cycles and is equal to approximately 54 years 33 days. Because it is nearly an integral number of days in length, two eclipses separated by 1 exeligmos (= 3 Saroses) not only share all the characterists of a Saros, but also take place in approximately the same geographic location.
The Saros panorama below is arranged in horizontal rows of 3 eclipses. So one eclipse to the left or right is a difference of 1 Saros cycle, and one eclipse above or below is a difference of 1 exeligmos. By scanning a column of the table, it reveals how the geographic visibility of eclipses separated by an exeligmos slowly changes.
- Click on any figure to go directly to the EclipseWise Prime Page for more information, tables, diagrams and maps. Key to Lunar Eclipse Figures explains the features in these diagrams.
For more information on this series see Statistics for Lunar Eclipses of Saros 161 .